Vítejte, dnes je
pátek
22.
listopad
2024
Odborný časopis a portál zaměřený na vývoj a výrobu elektroniky Účel všech systémů pro návrh plošných spojů je velmi podobný, a již to je přirozeným důvodem, pro který libovolné dva z nich obvykle mají více vlastností navzájem blízkých než rozdílných. K tomu bezpochyby přispívá i vzájemná konkurence, která jejich výrobce často vede k tomu, postupně si do svého factsheetu přidávat tytéž položky, jaké tam uvádějí ostatní.
O to zajímavější může být pohled na ty rysy, jimiž je některý návrhový systém unikátní. V systému Formica jedním z takových rysů jsou především množinové operace. Jsou tam (hlavně z důvodu jednodušší struktury databáze popisující DPS) implementovány poněkud výrazněji v editoru plošných spojů než ve schematickém editoru. Jelikož nemusí být na první pohled zřejmé, co se pod tímto mírně odrazujícím pojmem skrývá, v následujícím textu se na množinové operace podíváme krok za krokem. Pro přehlednost však budeme dělat kroky jen kratičké a užijeme k nim právě editaci plošných spojů.
V systému Formica desku plošného spoje tvoří prvky pouze čtyř druhů: pájecí body, segmenty spojových čar, kruhové oblouky a nápisy. (Součástky jsou – zhruba řečeno – jen agregace prvků uvedených druhů.) Každý prvek obsahuje bit (vlajku) zaznamenávající jeho označení; je-li prvek označen, je zobrazován zvýrazněný (tj. zpravidla světlejší). Stejný bit obsahují i jednotlivé součástky. „Označený“, „zvýrazněný“ a „vybraný“ jsou ve Formice synonyma, která v dalším textu budeme libovolně zaměňovat.
Nejjednodušší je prvky vybírat interaktivně, v grafickém editoru: kupříkladu lze označit prvek nebo součástku pod ukazatelem, spoj či spojku pod ukazatelem, všechny pájecí body v síti (netu), na kterou uživatel ukáže, anebo všechny prvky v obdélníkovém okénku vytvořeném ukazatelem. K tomu slouží několik režimů ukazatele (které mají ve Formice obdobný zásadní význam, jako v jiných systémech příkazy). Ty pro usnadnění práce navíc fungují vždy tak, že označení objektu překlápějí – není-li zvýrazněný, označí jej a zvýrazněný naopak z výběru odstraní. S částečně zvýrazněnými objekty, např. se spojem tvořeným více segmenty, z nichž jsou zvýrazněny jen některé, zacházejí podle toho, zda je zvýrazněn prvek pod ukazatelem. Výběr je kumulativní, označované prvky jsou v těchto režimech vždy přidávány k již označeným.
Také některé složitější příkazy, např. kontrola izolačních vzdáleností nebo hledání zkratů, podávají (vedle stručné textové zprávy) výsledek i v podobě označení příslušných prvků. Podobně může autorouter nově navržené spojky zároveň označovat, aby je odlišil od původních.
Dosud popsané funkce se nicméně od funkcí jiných návrhových systémů liší spíše jen tím, jak jsou zařazeny do kontextu ostatních příkazů. Podstatný rozdíl je ještě v tom, že označení prvků je permanentní (ačkoliv se neukládá do souborů na disku); nezaniká ukončením příkazu, který je vyvolal. Avšak teprve zde začíná popis těch vlastností, kterými je systém Formica unikátní.
Vedle interaktivního označování Formica nabízí několik desítek příkazů pro hromadný výběr prvků dle rozmanitých kritérií. Z rozsahu článku by se vymykalo zde vyjmenovávat všechny příkazy a s nimi korespondující kritéria, proto uvedeme pouhé ilustrativní ukázky. Příslušným příkazem lze vybrat např. všechny:
Vyjádřeno matematickými pojmy z prvních semestrů elektrofakulty (a ostatně též leckterých středních i základních škol) tvoří všechny prvky desky množinu, jejíž podmnožinou jsou ty označené. Těm laskavým čtenářům, kteří se snad s pojmem množin nesetkali (anebo naopak setkali a uchovali si děsivé vzpomínky) se autor upřímně omlouvá. Přesto však jsou operace nad množinami (a s nimi korespondující booleovské operace, jež zná každý programátor a každý elektronik, který se kdy zabýval číslicovou technikou) nejpohodlnějším i nejintuitivnějším nástrojem, jak příslušné funkce systému Formica popsat.
Jakmile však jsou v systému implementována takováto kritéria výběru, je přirozené i relativně snadné zajít ještě o krok dále. Je-li S množina označených prvků a Q množina, kterou definuje příslušné kritérium, všechny výše zmíněné příkazy přidávají prvky vyhovující kritériu k množině již označených, čili počítají sjednocení množin, S := S Q.
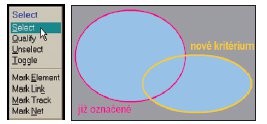
Obr. 1 Příkaz Select / Select přidá další prvky k již označeným
Co když však potřebujeme vybrat prvky, které vyhovují více kritériím zároveň? V takovém případě poslouží průnik množin, S := S Q.
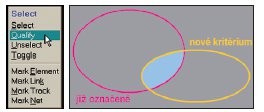
Obr. 2 Příkaz Select / Qualify označené prvky omezí novým kritériem
Malý příklad: Nejprve zvýrazníme všechny spojové čáry užší než 0,15 mm a pak stávající označení prvků omezíme pouze na vrstvu číslo 23. Výsledkem (pokud na počátku nebyly označeny žádné prvky) bude, že označeny budou všechny segmenty spojové čáry na vrstvě 23 užší než 0,15 mm (a žádné další prvky). A jestliže místo nich potřebujeme vybrat všechny segmenty spojové čáry užší než 0,15 mm kromě těch, které jsou na vrstvě 23? Místo operace průniku množin užijeme množinového rozdílu, S := S \ Q, jehož výsledkem bude množina právě těch prvků, které jsou v S a nejsou v Q.
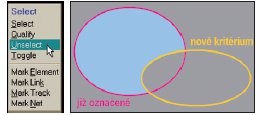
Obr. 3 Příkaz Select / Unselect od označených prvků ubere ty, které vyhovují kritériu
Poslední množinovou operací, kterou systém Formica nabízí, je symetrická diference S := S Q, jež vypočte množinu těch prvků, které byly v právě jedné z množin S a Q.
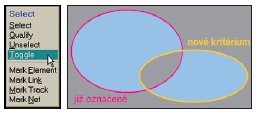
Obr. 4 Příkaz Select / Toggle obrátí označení prvků splňujících kritérium
Jakkoliv záhadně může předešlá formulace znít, symetrická diference prostě obrací označení těch prvků, které vyhovují kritériu Q. Jejím častým užitím je náhrada nějakého kritéria, jež není implementováno přímo. Potřebujeme-li kupříkladu označit všechny spojové čáry širší než zadaná hodnota, nejprve označíme všechny užší a pak obrátíme označení všech spojových čar.
Jak jsou tyto čtyři množinové operace implementovány v systému menu? Samotná kritéria se nacházejí v podstromu menu, tvořeném desítkami příkazů v několika podmenu. Do tohoto podstromu však uživatel může vstupovat skrz čtyři různé příkazy, totiž Select / Select (Add), Select / Qualify (Intersect), Select / Unselect (Subtract) a Select / Toggle (Invert).
Jenže, k čemu je to všechno dobré? Chápeme-li desku a prvky na ní množinově, plyne nám z toho vůbec nějaký prospěch?
Ve skutečnosti může přinést podstatný užitek již samotné označení a někdy dokonce i pouhá informace, zda nějaké prvky označeny jsou. Vrátíme-li se k výše zvolenému příkladu, co jestli čáry užší než 0,15 mm nejsou na (sítotiskové) vrstvě 23 vyrobitelné? V tom případě nám poskytne důležitou informaci už zjištění, zda je taková podmnožina prázdná, jinými slovy to, zda po provedení zmíněných příkazů je počet označených prvků nula, což indikuje číslo v příslušném informačním okně.
Samozřejmě ještě praktičtější může být vidět, které prvky jsou označeny: například poté, co příkaz pro kontrolu izolačních vzdáleností označil prvky, které spolu kolidují. Nejsou-li na složitější desce v malém zvětšení zvýrazněné prvky vidět na první pohled, lze je tam najít k tomu určenými příkazy.
Možnosti množinových operací ovšem nekončí tím, že nějakou podmnožinu prvků desky označíme a tím zvýrazníme. Zůstaneme-li u téhož příkladu s vyrobitelností DPS, nejjednodušší je příliš úzké čáry prostě rozšířit. K tomu stačí jediná věc, totiž všem označeným prvkům vnutit určitou šířku, třeba 0,2 mm. Formica má mj. právě tento příkaz: příkaz Edit / Change / Line Type nastaví dále zadanou šířku všem aktuálně vybraným prvkům, které atribut šířky mají; případné též označené objekty ostatních druhů prostě ignoruje. Obdobně, tedy podmnožině vybraných prvků, lze nastavovat logický typ (padstack) pájecího bodu, vrstvu, výšku znaků, orientaci a zrcadlení nápisů nebo fixování součástek. (Každý z nich se automaticky omezuje na ty druhy prvků, na něž jej lze aplikovat.) Další příkazy dovolují podmnožinu vybraných prvků kopírovat, odtahovat, přesouvat či mazat. (I tyto příkazy automaticky vynechají objekty, které nejde editovat samostatně, např. prvky součástek nebo zafixované součástky.)
Pojem ortogonality jsem si vypůjčil z instrukčních souborů procesorů (a tam se zas zřejmě dostal z lineární algebry). Možnost nastavit šířku čáře či kopírovat nějakou skupinu objektů jistě má každý návrhový systém. Avšak zatímco jiné systémy kupříkladu nastavují šířku čáry, na niž uživatel ukázal pravým tlačítkem myši, nebo kopírují objekty, které bezprostředně předtím zahrnul do okénka, Formica dovoluje pracovat s výběrem (tedy s podmnožinou označených prvků) i zcela nezávisle na tom, jakým způsobem či postupem tento výběr vznikl. Operace (tj. funkce a příkazy) tak jsou ortogonální k operandům, tedy k podmnožinám prvků, na něž jsou aplikovány (přirozeně s podmínkou, že jsou na prvky příslušných druhů vůbec aplikovatelné).
Tato nezávislost příkazu na výběru prvků, s nimiž pracuje, tj. tato vzájemná nezávislost operace a operandu, představuje novou kvalitu, která Formice dovoluje upustit od individuálního uzpůsobování příkazů operandům (jako je např. přidávání/ubírání prvků do/z kopírovaného okénka). V praxi to při stejné užitné hodnotě systému znamená ušetřit tucty příkazů, jejichž jednotlivé zvláštnosti by programátor musel implementovat a uživatel se naučit ovládat.
Mimochodem, množinové operace představují cosi jako postfixový zápis. Formica má příkazy jak pro editování (kopírování, odtahování, mazání) okénka, tak i podmnožiny. Jenomže zatímco v prvním případě si uživatel nejdříve volí příkaz (operaci) a až po něm operand (umísťuje okénko na desce), ve druhém je tomu naopak: operand již existoval v podobě podmnožiny objektů označených užitím nějakých dřívějších příkazů, operaci si uživatel zvolí až následně.
Na bit v jednotlivých prvcích, který určuje označení a zvýraznění, můžeme také pohlížet jako na jednobitovou vlajku. Množinové operace sjednocení, průniku, rozdílu a symetrické diference pak lze též popsat známými booleovskými operátory nad těmito vlajkami:
s := s or q ,
s := s and q ,
s := s and not q ,
s := s xor q .
Proč by však nemohl každý prvek mít takovýchto vlajek více? Všechny zároveň by je sice šlo vizualizovat jen s obtížemi, ale skrytě jich v libovolném prvku snadno může být několik. Testovací verze systému Formica 4.40 (určené zejména pokročilejším uživatelům) tak mají vedle vlajky svázané se zvýrazněním prvků ještě další čtyři, pojmenované A, B, C a D.
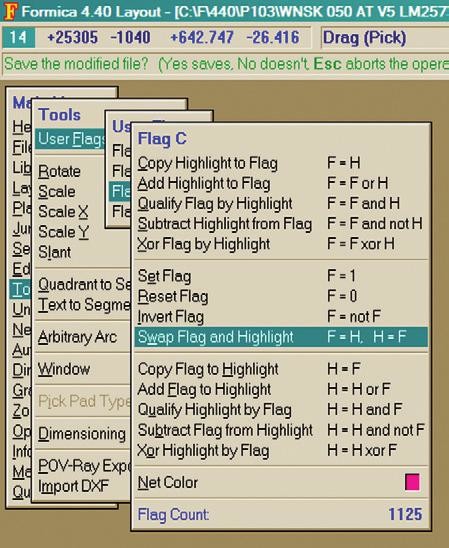
Obr. 5 Menu Tools / User Flags / Flag A...D nabízejí celkem 14 příkazů pro operace s uživatelskými vlajkami a základní vlajkou pro výběr. (Vždy dvě pětice příkazů jsou navzájem symetrické.)
S každou z těchto uživatelských vlajek je (vždy u veškerých prvků na desce najednou) možno provádět běžné logické operace vůči výchozí vlajce (v menu uváděné jako H), definující základní zvýraznění a označení; navíc ji lze nastavovat, nulovat, přesouvat do vlajky H (a opačně) nebo ji s ní vyměňovat. Přehled všech dostupných operací vyplývá z obrázku příslušného podmenu menu Tools; podrobnější diskuse by překračovala rozsah článku.
Obr. 6 Ukázka DPS v editoru systému Formica
Mohou takovéto operace fungovat (a být užitečné) i prakticky? A jestli ano, proč nenacházíme nic podobného v jiných návrhových systémech? Částečnou odpovědí na druhou otázku snad může být, že množinové operace jsou v systému Formica provázány s jeho ostatními unikátními vlastnostmi. Jednou z nich je jednoduchost databáze, zmíněná v úvodu článku. Dalším takovým konceptem je dynamická konektivita: spoje neexistují jako samostatné objekty, nýbrž jsou dynamicky sestavovány z prvků umístěných na desce, kdykoliv je se spoji jako takovými třeba pracovat. Ještě větší význam pro množinové operace mají „prostupné“ součástky: jejich jednotlivé prvky z nich sice nemohou být odstraněny (ani přidány), ale v jejich rámci je lze různými způsoby editovat i po umístění součástky na desku.
Užitečnost ovšem závisí i na přístupu uživatele, totiž na tom, zda bude v pojmech množinových operací uvažovat. Začne-li, množinové operace se mu brzy budou jevit až překvapivě intuitivní; ostatně též podstatně jednodušší, než přečíst tento článek. A najít cestu, jak je v konkrétní situaci užít, pro něj bude daleko snazší, než příslušný postup vysvětlit slovy.
Množinové operace si lze samozřejmě také vyzkoušet s volně šiřitelnou verzí systému Formica, dostupnou na www.formica.cz. O koncepci systému se tam čtenář může dozvědět více na stránce Principy v pozadí (www.formica.cz/principy.html).
