Optimalizace modelu vícevrstvé DPS při mechanickém testování

Úvod

Vývoj nových elektronických výrobků je v dnešní době úzce spojen s oblastí spolehlivosti těchto přístrojů. S ohledem na vzrůstající počet mobilních zařízení se stále více výrobců zaměřuje na ověření mechanických vlastností, k čemuž lze využít jak softwarové simulační nástroje, tak experimentální měření. Konkrétně je při těchto testech zjišťována rezonanční frekvence DPS a následně také maximální velikost vychýlení pro dané uspořádání. Tyto parametry jsou určeny mechanickými vlastnostmi DPS, rozmístěním součástek a také způsobem uchycení. Pokud chceme optimalizovat konkrétní systém z hlediska rezonance, musíme stanovit nejlepší možnost návrhu jak z pohledu dispozičního uspořádání, tak také z hlediska materiálového. Pro optimalizaci je vhodné využít moderních technologií a realizovat ji prostřednictvím počítačových simulací. Tímto krokem jsme schopni nejen ušetřit značné náklady, ale také ověřit různé možnosti, které by bylo velice obtížné realizovat experimentálními metodami.

Optimalizace modelu DPS

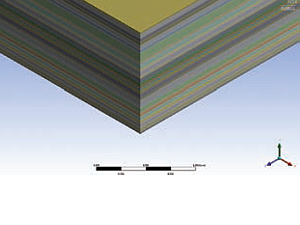
Při ověřování mechanických vlastností pomocí simulací je jedním z klíčových úkolů vytvoření odpovídajícího virtuálního modelu; model jednoduché DPS je vidět na obr. 1. Ten by měl v ideálním případě být identický s reálným zařízením. Avšak počítačové modelování má svá omezení, se kterými je během přípravy modelu potřeba počítat. Tato omezení spočívají jednak ve schopnosti přenést všechny okolní podmínky, které ovlivňují chování sestavy, do jádra programu a pak také v hardwarových možnostech, které máme k tomuto účelu k dispozici.

Obr. 1 Virtuální model DPS uchycené pomocí šroubů

Okolními podmínkami je v tomto případě myšleno například utažení šroubů, způsob uchycení desky či nastavení zrychlení soustavy. Všechny tyto parametry se řídí nastavením reálného testu či údajů poskytnutých zadavatelem.

Jak bylo zmíněno v úvodu, můžeme počítačovou simulací reálných struktur ušetřit značné finanční prostředky i čas. Míra těchto úspor se však odvíjí od hardwarového vybavení, které máme k dispozici, neboť simulace jsou velice náročné na výpočetní výkon i na operační paměť PC. Avšak i při použití výkonné výpočetní techniky může simulace trvat několik hodin, v závislosti na složitosti modelu. Z tohoto pohledu je tedy vhodné daný model optimalizovat či zjednodušit.

V praxi se kromě jednoduchých desek často setkáváme s vícevrstvými deskami, které jsou z pohledu simulace velice náročné na modelování a je tedy nutné jejich model patřičně upravit. Pokud budeme pracovat s neosazenou deskou či pokud je rozmístění součástek souměrné, můžeme využít symetrie v jedné či více osách.

Obr. 2 Čtvrtmodel desky (vlevo) a kompletní virtuální model desky (vpravo)

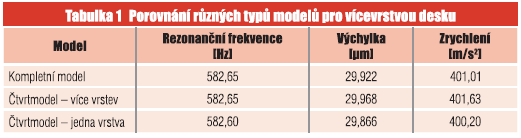
Na obr. 2. je znázorněna tato úprava modelu, kde byla vytvořena čtvrtina modelu. Na stranách řezu byla nastavena souosost; a to v ose Z a X. Pro oba modely byla vytvořena totožná modální a harmonická analýza a jejich výsledky byly porovnány (tabulka 1).

Kromě využití symetrie je další možností úpravy modelu také jeho zjednodušení z hlediska počtu vrstev. Pokud modelujeme každou vrstvu zvlášť, je velice náročné vytvořit síť konečných prvků, díky které se model diskretizuje. Ta bývá často nesouměrná a obsahuje velké množství elementů. Proto lze DPS modelovat jako jednolitou vrstvu, jejíž materiálové vlastnosti upravíme tak, aby se výsledek shodoval s vícevrstvou variantou. Ačkoli se takto zjednodušený model při úpravách chová mírně odlišně od vícevrstvého modelu, jsme schopni vypočíst základní údaje pro různé úpravy DPS. Na základě porovnání těchto úprav dále stanovíme finální verzi modelu, kterou realizujeme vícevrstvou strukturou.

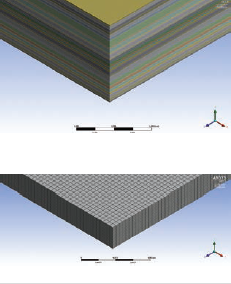
Obr. 3 Kompletní model vícevrstvé desky (nahoře), modifikovaný model s jednou vrstvou (dole)

Zjednodušený model lze vidět na obr. 3. Aby bylo možné simulovat více vrstev v tloušťce desky, využili jsme sítě konečných prvků, kdy u celistvého modelu byl nastaven stejný počet elementů, jako byl počet vrstev u zmiňované DPS. Výsledky pro tento model jsou v tabulce 1 (Čtvrtmodel – jedna vrstva). Kromě úspory času jsme schopni díky tomuto kroku ověřit výsledky simulace pomocí analytického výpočtu, který by byl značně komplikovaný, pokud bychom pracovali s kompletní vícevrstvou strukturou.

Pro analytický výpočet jsou upravená materiálová data desky plošných spojů modifikované verze modelu shrnuta v tabulce 2.

Analytický výpočet se následně řídí stejnými rovnicemi jako v případě jednovrstvé desky [1]. Rezonanční frekvence se stanoví pomocí faktoru tuhosti desky D a vztažné hmotnosti M, ty lze vyjádřit jako:

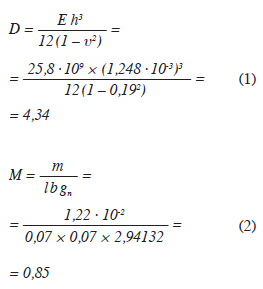
kde E je Youngův modul pružnosti, h je tloušťka desky, υ Poissonova konstanta, m je celková hmotnost desky, l délka desky, b šířka desky a g_n tíhové zrychlení.

Pokud známe tyto hodnoty, můžeme vypočíst výslednou rezonanční frekvenci f_n, podle následujícího vzorce:

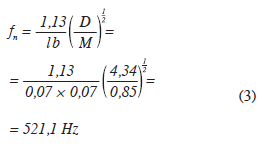
Získaná hodnota 521,1 Hz se liší od hodnoty simulace zhruba o 10 %, tento rozdíl je dán zejména rozdílným způsobem výpočtu, zaokrouhlením a také mírou zjednodušení modelu. Ačkoli je chyba poměrně značná, při úpravách modelu zůstává rozdíl mezi hodnotami konstantní. Na základě této zkušenosti tedy můžeme tímto způsobem určit rezonanční frekvenci daleko rychleji než při využití komplexní simulace, která v případě vícevrstvých desek může trvat i několik hodin/dní (v závislosti na použitém hardwaru a složitosti desky).

Závěr

V článku je prezentován způsob optimalizace virtuálního modelu při řešení problému mechanických vibrací pomocí počítačových simulací. Značné množství času lze ušetřit využitím symetrie DPS, přičemž je možné v této konfiguraci ověřit například uchycení modelu či symetrické rozestavení součástek na desce. Následně pak tyto znalosti mohou být přeneseny do kompletního modelu. Obdobně je tomu i u druhého způsobu zjednodušení, jenž byl představen. Zde je vícevrstvá struktura nahrazena celistvou vrstvou s upravenými vlastnostmi. Touto úpravou se nejen ušetří značný čas potřebný k výpočtu, ale simulace může být ověřena pomocí analytického výpočtu a lze se tak ujistit o správnosti výsledné hodnoty rezonanční frekvence.

Použitá literatura:

[1] STEINBERG, D. S., Vibration Analysis for Electronic Equipment, New York, Wiley-Interscience, 1988, 460 p.

[2] IVAN, L. a kol. Mechanical: Základy mechanické analýzy. Studijní materiály ke kurzu ANSYS Workbench Mechanical. SVSFEM 2009.

[3] OTÁHAL, A.; SZENDIUCH, I.; PSOTA, B. Mechanical testing of PCB using computer simulations. In 37th Int. Spring Seminar on Electronics Technology. Dresden: IEEE, 2014. s. 290-293. ISBN: 978-1- 4799-4455- 2.