Logický analyzátor M611: Teória a prax
Logický analyzátor je neodmysliteľným meracím prístrojom v predmete Elektronika – časť číslicová technika, ktorý sa vyučuje na stredných odborných školách zameraných na elektrotechniku. Logický analyzátor umožňuje, aby študenti videli súvislosti medzi signálmi v kombinačných aj sekvenčných obvodoch a na základe týchto súvislostí vedeli posúdiť správnu funkciu obvodu alebo diagnostikovať nesprávnu činnosť a vedeli obvod opraviť.
Článok je rozdelený na tri časti. V prvej je uvedený postup návrhu kombinačného obvodu a jeho meranie logickým analyzátorom, v druhej časti je uvedený postup návrhu sekvenčného obvodu a jeho meranie logickým analyzátorom a v tretej časti sú technické parametre logického analyzátora M611 od firmy ETC Žilina. Článok je určený študentom stredných odborných škôl zameraných na elektrotechniku, pre ktorých má byť článok ukážkou spojenia teórie – návrh obvodov a praxe – meranie obvodov logickým analyzátorom.
Kombinačné obvody
Kombinačné obvody sú veľmi rozšíreným typom číslicových obvodov. Okrem obvodov dodávaných vo forme integrovaných obvodov, ktoré plnia funkciu napríklad dekodérov, sčítačiek, multiplexorov atď. sa v praxi používajú aj obvody, ktoré vykonávajú špeciálne funkcie podľa požiadaviek používateľa. Chceme, napríklad, realizovať číslicový obvod, ktorého stav výstupov Y0, Y1 a Y2 bude závislý od stavov vstupov A, B a C tak, ako je to znázornené v pravdivostnej tabuľke na obr. 1. Na základe pravdivostnej tabuľky zostavíme Karnaughove mapy (obr. 1), do ktorých nakreslíme kontúry. Kontúram zodpovedajú logické funkcie v podobe súčtu súčinov premenných A, B a C. Logické funkcie sú pod Karnaughovými mapami. Tam sú aj funkcie, ktoré sme získali pomocou de Morganových pravidiel, aby sme obvod mohli realizovať pomocou hradiel NAND.
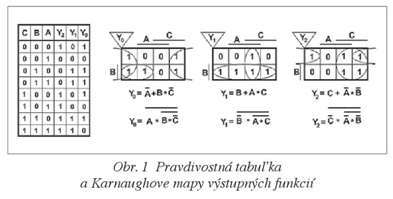
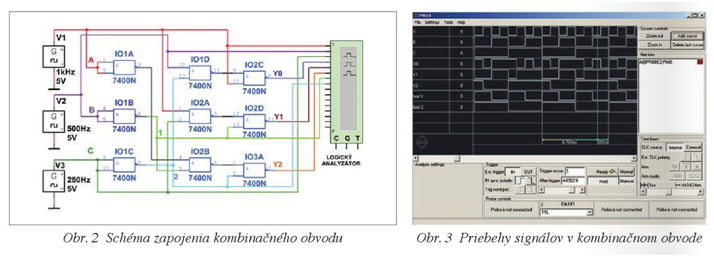
Schéma zapojenia číslicového obvodu je na obr. 2. Na obr. 3 je priebeh číslicových signálov získaných pomocou logického analyzátora M611. Žltým a zeleným kurzorom je vymedzený interval kombinácií vstupných signálov A, B a C od stavu 000 do stavu 111. Modrým kurzorom je označený stav, keď A = L, B = H a C = H. Tomu zodpovedajú stavy výstupov a stavy v bodoch 1 a 2, Y0= H, Y1= H, Y2= H, bod 1 = L a bod 2 = L.
Sekvenčné obvody
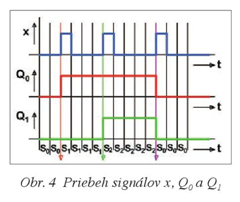
Sekvenčné obvody sú veľmi rozšíreným typom číslicových obvodov. Okrem obvodov dodávaných vo forme integrovaných obvodov, ktoré plnia funkciu napríklad preklápacích obvodov, počítadiel, registrov atď., sa v praxi používajú aj obvody, ktoré vykonávajú špeciálne funkcie podľa požiadaviek používateľa. Napríklad chceme realizovať sekvenčný obvod, ktorý bude pracovať nasledujúcim spôsobom. Obvod je v pokoji až dovtedy, kým nepríde prvý impulz signálu x. Vtedy prejde výstup Q0 z úrovne L do úrovne H, výstup Q1 zostáva v úrovni L. Po príchode druhého impulzu signálu x prejde výstup Q1 z úrovne L do úrovne H, výstup Q0 zostáva v úrovni H. Po príchode tretieho impulzu signálu x prejde výstup Q0 aj výstup Q1 z úrovne H do úrovne L. Priebeh signálov x, Q0 a Q1 je na obr. 4.
Návrh sekvenčného obvodu začneme tým, že z priebehu signálov x, Y0 a Y1 vypíšeme všetky stavy, ktoré signály x, Y0 a Y1 môžu nadobúdať. V našom príklade ide o tri stavy S0, S1 a S2, ktoré sú v tabuľke definujúcej stavy S a tá je na obr. 5. Na základe priebehov zostavíme tabuľku prechodov na obr. 5, z ktorej môžeme nakresliť graf prechodov, v ktorom sú okrem stavov znázornené aj prechody a podmienky, za ktorých k prechodu dôjde (obr. 5). Zostavíme tabuľku vnútorných stavov tak, že k jednotlivým prechodom priradíme ľubovoľné n-bitové číslo, ktoré sa nesmie opakovať a bude zodpovedať stavom výstupov Q. V našom príklade stačí dvojbitové číslo, lebo máme iba tri stavy (obr. 5). Do celkovej tabuľky, ktorá je na obr. 5, napíšeme tabuľku prechodov a stavy výstupov Q0 a Q1v čase n a n+1.
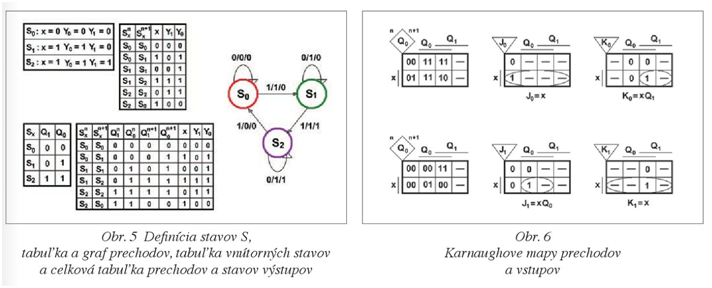
Z celkovej tabuľky zostavíme Karnaughove mapy prechodov pre výstupy Q0 a Q1, ktoré sú na obr. 6. Z nich zostavíme Karnaughove mapy vstupov preklápacích obvodov podľa toho, či budeme schému zapojenia realizovať pomocou preklápacích obvodov D, alebo JK (poprípade RS alebo T). Zvolíme preklápací obvod JK a napíšeme funkcie pre vstupy J0, J1, K0 a K1. Pre výstupy Y0 a Y1nemusíme robiť Karnaughove mapy, pretože rozloženie 0 a 1 výstupu Y0 je totožné s rozložením 0 a 1 výstupu Q0 v čase n+1. Podobne je to aj s výstupom Y1. Potom nakreslíme schému zapojenia, ktorá je na obr. 7. Na obr. 8 je priebeh logických signálov získaných pomocou logického analyzátora M611. V obr. 4 dochádza k prechodom výstupov Y0 a Y1 z L do H a naopak na nábežnú hranu signálu x, ale na obr. 8 dochádza k prechodu na zostupnú hranu signálu x. Je to dané tým, že preklápací obvod JK, ktorý bol použitý na realizáciu schémy zapojenia, preklápa na zostupnú hranu vstupného impulzu.
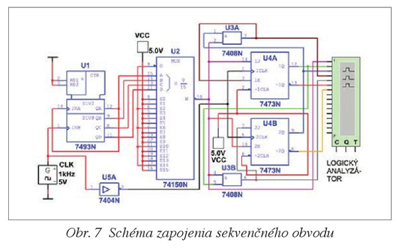

Technické parametre logického analyzátora M611
Logický analyzátor M611 patrí do skupiny meracích prístrojov, ktoré sa k počítaču pripájajú cez USB port alebo cez paralelný port. Na priame pripojenie na paralelný port slúži kábel opatrený konektormi, na pripojenie cez USB port je k dispozícii redukcia z paralelného portu na port USB. Logický analyzátor je napájaný do sieťového napájača, redukcia je napájaná z USB portu.
a) časová analýza:
- počet kanálov 32,
- frekvencia hodinových impulzov 2,5 kHz až 100 MHz,
- interné a externé spúšťanie,
- šírka interného spúšťacieho slova 32 bitov,
- nastavenie bitov interného spúšťacieho slova 1, 0, X,
- externé spúšťanie 1 bit na nábežnú alebo zostupnú hranu,
- výskyt spúšťacej udalosti nastaviteľný od 1 do 65 535,
- maximálna dĺžka záznamu je 524 280 slov,
- pozícia spúšťacieho slova v zázname kdekoľvek v kroku 8 slov,
- režim zberu jednorazový alebo opakovaný.
b) stavová analýza:
- počet kanálov 30,
- počet externých hodinových vstupov 1,
- blokovací signál (ARM) 1,
- maximálna frekvencia hodinových impulzov 50 MHz,
- šírka spúšťacieho slova 30 bitov,
- nastavenie bitov spúšťacieho slova 1, 0, X,
- maximálna dĺžka záznamu je 524 280 slov,
- pozícia spúšťacieho slova v zázname kdekoľvek v kroku 8 slov,
- externé spúšťanie 1 bit na nábežnú alebo zostupnú hranu.
Technické údaje sondy EA111:
- počet kanálov 8,
- oneskorenie < 10 ns,
- sklz medzi jednotlivými kanálmi < 1 ns,
- prahové napätie nastaviteľné 3,3 V CMOS, 5 V CMOS, TTL,
- rozsah vstupných napätí v režime 3,3 V CMOS je – 2 V až + 7 V,
- rozsah vstupných napätí v režime 5 V CMOS a 5 V TTL je – 2 V až + 7 V (prekročenie rozsahu napätí môže spôsobiť zničenie sondy).
Záver
Logický analyzátor M611 je merací prístroj, ktorý svojimi vlastnosťami vyhovuje požiadavkám stredných aj vysokých škôl zameraných na elektrotechniku. Rovnako dobre poslúži aj v profesionálne praxi a nájde uplatnenie aj v dielni pokročilého amatéra. Zvládnutie obsluhy logického analyzátora je dôležitým predpokladom na to, aby študenti vedeli v praxi diagnostikovať číslicové obvody a zariadenia. Hlavne preto, že je to jediný spôsob, ako zviditeľniť číslicové priebehy naraz v x miestach obvodu a sledovať súvislosti medzi nimi. Na kreslenie schém, obrázkov a tabuliek bol použitý program MultiSIM 13.0.1. Bližšie informácie o logickom analyzátore M611, ako aj o ďalších výrobkoch firmy ETC, získate na adrese www.etc.sk.




