Vítejte, dnes je
úterý
31.
prosinec 2024
Odborný časopis a portál zaměřený na vývoj a výrobu elektroniky V roku 1933 navrhol a publikoval Philiph Smith grafický nástroj zjednodušujúci počítanie a riešenie problémov súvisiacich s transformáciou impedancie na vedení. Keďže v tom čase (a ešte dlhé roky potom) nebola výpočtová technika na dostatočnej úrovni, Smithov diagram sa stal jednou z najpoužívanejších pomôcok pri vývoji vysokofrekvenčných obvodov. Aj keď v súčasnosti moderné simulačné programy riešia dané úlohy oveľa efektívnejšie, Smithov diagram ostáva naďalej veľmi užitočnou pomôckou hlavne pri zobrazení výsledkov meraní a simulácií.
Smithov diagram je zobrazenie činiteľa odrazu v polárnych súradniciach, do ktorého je potom namapovaná impedančná (z = r + jx) a/alebo admitančná (y = g + jb) rovina. Označenie jednotlivých premenných malými písmenami hovorí, že všetky hodnoty na diagrame sú normalizované k referenčnej impedancii systému Z0 (najčastejšie 50 Ω).
Ako bolo spomínané v predchádzajúcom článku o S-parametroch, činiteľ odrazu Γ na určitom porte vyjadruje, aká časť dopadajúcej vlny sa z príslušného portu odrazí, a vieme ho vypočítať zo vzťahu
kde z = r + jx je normovaná impedancia pripojená k príslušnému portu (z = Z/Z0). Vo väčšine aplikácií sa snažíme preniesť čo najväčší výkon do záťaže, t. j. aby sa čo najmenšia časť vlny odrazila späť, a teda dosiahnuť čo najmenšiu hodnotu činiteľa odrazu (obr. 1).
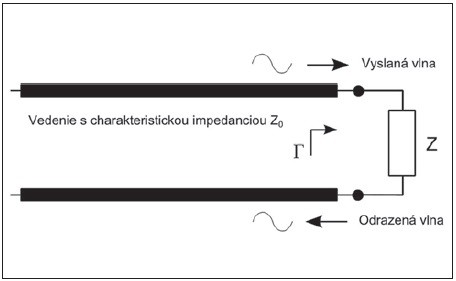
Obr. 1 Znázornenie vlnových pomerov na vedení
Činiteľ odrazu je vyjadrený komplexným číslom, ktoré má pre všetky kladné hodnoty r absolútnu hodnotu v intervale <0;1> a fázu <–180°;180°>. Jeho grafickým zobrazením v polárnych súradniciach je teda kruh s polomerom 1.
Na obr. 2 je zobrazená Γ-rovina s vyznačenými niekoľkými významnými bodmi. Bod A, sústredený priamo v strede kruhu, zobrazuje dokonalé prispôsobenie, keď Z = Z0. Celá vlna sa absorbuje v záťaži a teda | Γ | = 0. Bod B predstavuje skratovaný port, t. j. Γ = 1 ∠ 180°. V tomto prípade sa celá vlna od záťaže odrazí a s opačnou fázou sa bude šíriť späť po vedení. Podobne, avšak bez zmeny fázy, sa celá vlna odrazí aj v prípade bodu C, ktorý zobrazuje port v stave naprázdno, a teda Γ = 1 ∠ 0°.
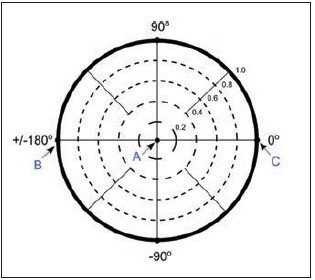
Obr. 2 Zobrazenie Γ-roviny
Impedančná rovina predstavuje všetky komplexné impedancie Z, ktoré môžu byť privedené k skúmanému portu. Najčastejšie sa zobrazuje v karteziánskych súradniciach, ako to vidíme na obrázku 3 vľavo.
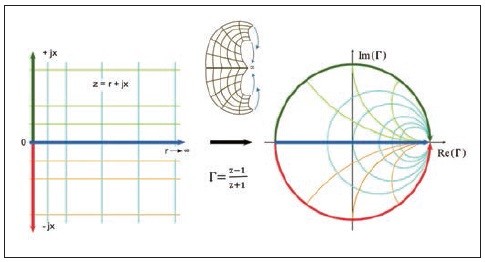
Obr. 3 Mapovanie impedančnej roviny do Γ-roviny
Keďže hodnota činiteľa odrazu a impedancie navzájom súvisia, bolo by dobré vedieť nejakým spôsobom tieto 2 korešpondujúce hodnoty odčítať priamo z jedného obrázka. To najľahšie dostaneme namapovaním z-roviny do Γ-roviny.
Výraz „mapovanie“ tu znamená, že každý bod v z-rovine sa na základe vzájomného vzťahu medzi činiteľom odrazu a impedanciou zobrazí v Γ-rovine. Pre lepšiu názornosť celej transformácie zobrazíme toto mapovanie graficky. (Na obrázku 3 je zobrazené iba mapovanie polroviny impedancií s kladnou reálnou časťou (r ≥ 0), čo je postačujúce pre väčšinu aplikácii. Každopádne, transformácia platí aj pre záporné r.)
Z obrázka 3 vidíme, že celá pravá polrovina z-roviny, zahŕňajúca všetky impedancie s kladnou reálnou časťou, sa namapuje dovnútra kruhu v Γ-rovine. Čisto rezistívne impedancie (jx = 0 – na obr. 3 zobrazené ako polpriamka nakreslená modrou farbou) sa namapujú do jedinej rovnej úsečky v Smithovom diagrame, pričom bod r = 0 tvorí ľavý okraj úsečky a r∞ pravý. Čisto reaktívne impedancie (r = 0 – na obr. 3 zobrazené ako polpriamky nakreslené zelenou a červenou farbou) tvoria v Γ-rovine kružnicu totožnú s kružnicou | Γ | = 1. Kružnice s ich stredmi na reálnej osi predstavujú impedancie s konštantnou reálnou časťou (r = konšt. – na obr. 3 zakreslené cyánovou farbou). Horizontálne priamky v z-rovine, zobrazujúce impedancie s konštantnou reaktívnou zložkou, sa namapujú do Γ-roviny ako oblúky. Induktívne reaktancie sa zobrazia v hornej polovici (+jx – na obr. 3 nakreslené zelenou farbou) a kapacitné v dolnej (−jx – na obr. 3 nakreslené oranžovou farbou).
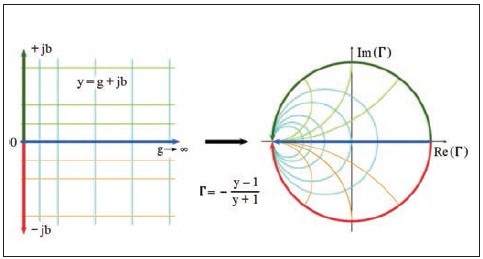
Obr. 4 Mapovanie admitančnej roviny do Γ-roviny
Analogicky by sme vedeli namapovať do Γ-roviny aj admitančnú rovinu y = g + jb (obr. 4). Takto dostávame konečnú podobu Smithovho diagramu (obr. 5). Praktické využitie Smithovho diagramu si ukážeme na príklade návrhu prispôsobovacieho člena v nasledujúcej časti článku.
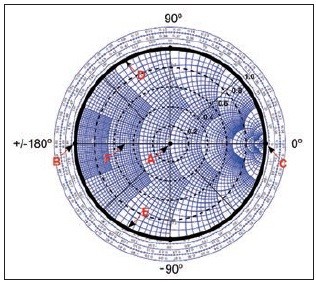
Obr. 5 Normalizovaný impedančný Smithov diagram s vyznačenými dôležitými bodmi
Úlohou impedančných prispôsobovacích obvodov je upraviť impedanciu zdroja a/ alebo záťaže na požadovanú hodnotu podľa potreby danej aplikácie.
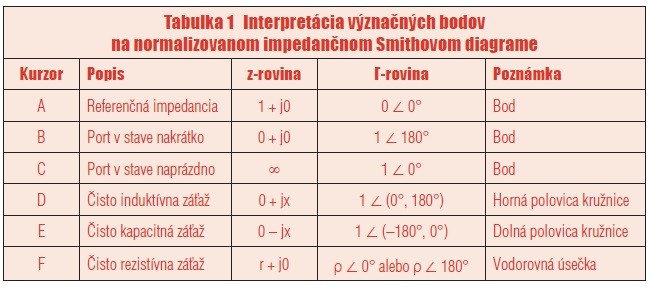
Tabulka 1 Interpretácia význačných bodov na normalizovanom impedančnom Smithovom diagrame
Impedančné prispôsobenie si najčastejšie spájame s dosiahnutím stavu, keď sa impedancia zdroja rovná konjugovanej hodnote impedancie záťaže. Dá sa jednoducho dokázať, že v takomto prípade dosiahneme maximálny prenos výkonu zo zdroja do záťaže. Ako zdroj či záťaž sa tu myslí anténa, zosilňovač, vedenie alebo ľubovoľný iný aktívny či pasívny prvok (pozrite obr. 6). Pri praktickom návrhu definujeme kvalitu prispôsobenia (inými slovami ako presne má byť dosiahnutá „rovnosť“ impedancií) pomocou parametra S11 pri jednoportovom obvode, prípadne aj S22, S33... pri viacportových obvodoch. Ako bolo uvedené v predchádzajúcom článku, parameter S11 vyjadruje pomer odrazenej vlny k dopadajúcej vlne na porte 1. Čím je jeho absolútna hodnota menšia, tým je port lepšie prispôsobený. Aby sme nemuseli pracovať s príliš malými desatinnými číslami, často sa udáva hodnota | S11 | v decibeloch, pričom platí | S11 | dB = 20 × log(| S11 |) .
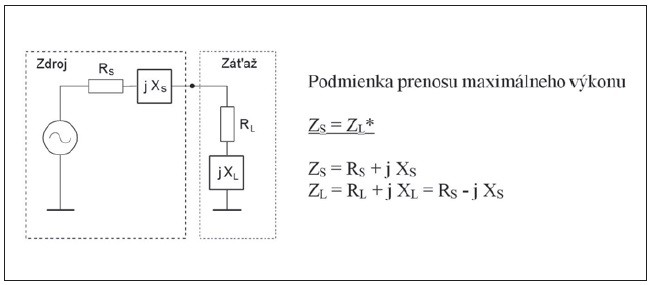
Obr. 6 Impedančné prispôsobenie na dosiahnutie maximálneho prenosu výkonu
Okrem požiadavky maximálneho prenosu výkonu existuje množstvo ďalších dôvodov na použitie impedančného prispôsobenia. Pri návrhu zosilňovača môžeme potrebovať prispôsobiť vstup aktívneho prvku na dosiahnutie minimálneho šumového čísla, prípadne jeho výstup na minimálne skreslenie. Rovnako môžeme využiť impedančné prispôsobenie na zabezpečenie stability zosilňovacieho prvku atď. Týmto prípadom sa však v tomto článku nebudem venovať.
Prispôsobovacie obvody môžeme rozdeliť z hľadiska metód návrhu na úzkopásmové a širokopásmové.
S úzkopásmovými obvodmi vieme dosiahnuť takmer ideálne prispôsobenie pri jednej frekvencii. Ukážeme si, že na úzkopásmové prispôsobenie akejkoľvek komplexnej impedancie postačuje kombinácia dvoch prvkov (čo však neznamená, že použitie dvojprvkového prispôsobovacieho člena je vždy najlepšie riešenie). Pri širokopásmovom impedančnom prispôsobení zväčša tolerujeme aj o niečo väčšie impedančné odchýlky, avšak v oveľa väčšom frekvenčnom pásme.
Kvôli minimalizácii strát sa snažíme navrhovať prispôsobovacie obvody kombináciou indukčností, kapacít a transformátorov s čo najvyššou kvalitou. Z tohto istého dôvodu sa na impedančné prispôsobenie využívajú rezistory len vo výnimočných prípadoch.
Predpokladajme, že chceme dosiahnuť maximálny prenos výkonu z vedenia do antény. To znamená, že potrebujeme zabezpečiť, aby vstupná impedancia antény bola pri požadovanej frekvencii (napríklad 433 MHz) rovná charakteristickej impedancii vedenia (napr. 50 Ω). Pre našu potrebu si zadefinujeme požadovanú hodnotu S11 ≤ −20 dB. Návrh takéhoto prispôsobovacieho obvodu je pomerne jednoduchý a určite sa dá zvládnuť aj ručne. Mojím cieľom je však na tomto príklade ukázať praktické využitie simulačných programov pri návrhu vysokofrekvenčných obvodov. Simulačný program použitý v tomto článku má názov RFsim99 a je voľne dostupný, bez akýchkoľvek licenčných poplatkov.
Na začiatku návrhu si musíme zistiť skutočnú vstupnú impedanciu použitej antény pri danej frekvencii. V ideálnom prípade si ju odmeriame vektorovým vektorovým analyzátorom. Ak nemáme k dispozícii potrebné meracie zariadenie, musíme použiť katalógovú hodnotu uvádzanú výrobcom.
Následne si na základe získaných dát určíme jednoduchú náhradnú schému antény v okolí požadovanej frekvencie. V našom príklade nech má anténa pri frekvencii 433 MHz vstupnú impedanciu Z = 189 + j66. Simulačná schéma bude potom vyzerať podobne ako na obr. 7. Keďže navrhujeme iba prispôsobenie medzi vedením a anténou, tak namiesto vedenia môžeme použiť iba port s impedanciou 50 Ω.
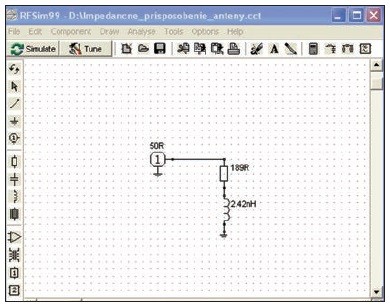
Obr. 7 Simulačná schéma k návrhu impedančného prispôsobenia.
Po spustení simulácie dostaneme znázornenie danej impedancie na Smithovom diagrame, ako aj zodpovedajúcu hodnotu parametra S11 = −5,95 dB (pozrite obr. 8). Po zobrazení vstupnej impedancie antény na Smithovom diagrame môžeme pristúpiť k návrhu zapojenia. Pripomeňme si, že naším cieľom je pridaním kapacitných a induktívnych prvkov dosiahnuť, aby vstupná impedancia antény v kombinácii s týmito prvkami bola ~50 Ω. V grafickom znázornení to znamená, že sa snažíme posunúť červený kurzor do stredu Smithovho diagramu. Zároveň budeme sledovať, že čím viac sa približujeme k stredu, tým menšia je hodnota parametra S11.
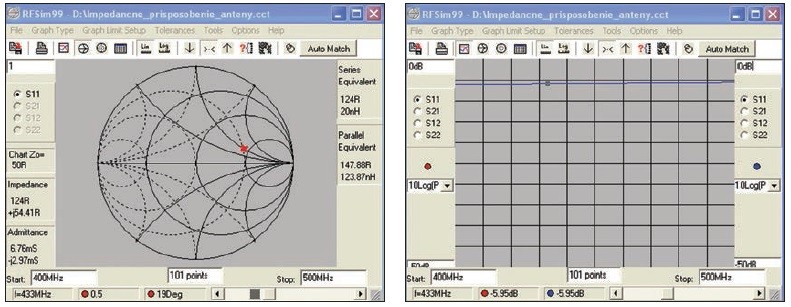
Obr. 8 Zobrazenie vstupnej impedancie antény a parametra S11 na Smithovom diagrame a v pravouhlých súradniciach.
Na vyriešenie danej situácie použitím dvoch prvkov máme 2 možnosti. Prvou možnosťou je pridaním paralelnej indukčnosti nastaviť vstupnú impedanciu do stavu Z = 50 + jXL. Graficky to znamená, že sa po kružnici konštantnej reálnej hodnoty admitancie posunieme na hornú polovicu kružnice prechádzajúcej stredom Smithovho diagramu (bod A). Induktívnu zložku impedancie potom vykompenzujeme pridaním sériovej kapacity, t. j. po kružnici konštantnej reálnej hodnoty impedancie dosiahneme stred Smithovho diagramu.
Druhou možnosťou je pridaním paralelnej kapacity nastaviť vstupnú impedanciu do stavu Z = 50 – jXC, t. j. posun na dolnú polovicu kružnice prechádzajúcej stredom (bod B). Kapacitnú zložku impedancie potom vykompenzujeme pridaním sériovej indukčnosti. Obe možnosti sú znázornené na obr. 9.
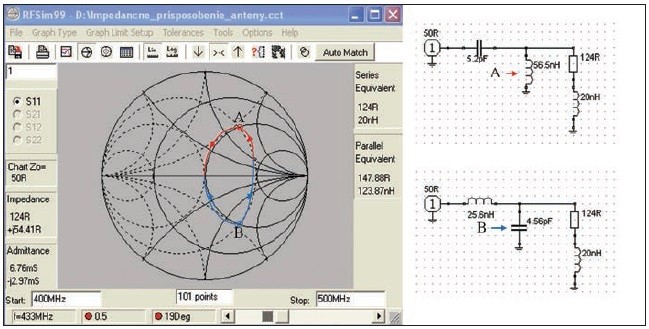
Obr. 9 Grafické znázornenie prispôsobenia antény.
Na záver nahradíme vypočítané hodnoty najbližšími reálnymi hodnotami súčiastok a skontrolujeme dosiahnutú presnosť prispôsobenia (pozrite obrázok 10).
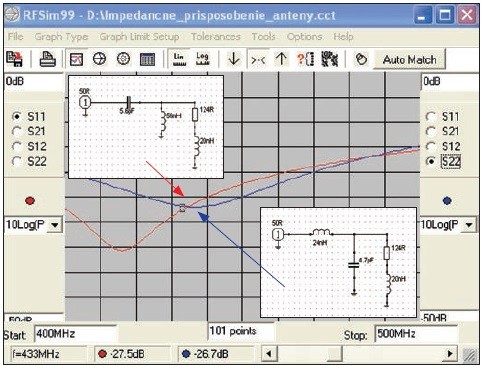
Obr. 10 Zobrazenie výslednej hodnoty parametra S11.
V našom prípade sme dosiahli hodnoty S11 = −27,5 dB, resp. −26,7 dB, čím sme splnili stanovené kritériá. Pre úplnosť treba poznamenať, že v reálnom návrhuby bolo treba zobrať do úvahy ďalšie veci, ako parazitné vlastnosti súčiastok, vplyv dosky plošného spoja, konektora, poprípade aj pripájacieho kábla.
Užitočnou pomôckou pri určení správnej kombinácie prvkov môže byť obr. 11. Tu si na základe polohy impedancie v impedančnej rovine môžeme vybrať potrebné zapojenie. Ak sa obraz impedancie nachádza v zelenej časti z-roviny, môžeme použiť zapojenie na danom obrázku. Toto následne vložíme do simulátora, pomocou ktorého určíme správne hodnoty daných súčiastok.
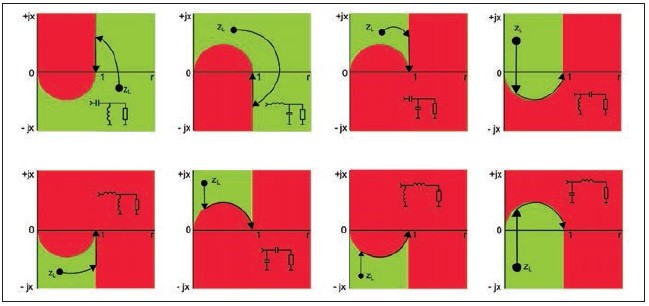
Obr. 11 Zapojenia prispôsobovacích obvodov podľa polohy normovanej impedancie v z-rovine
Poznámka:V prípade, že naším cieľom je prispôsobiť záťaž k inej impedancii, ako je referenčná impedancia Z0, potom sa snažíme pridávaním prvkov dosiahnuť na Smithovom diagrame bod zodpovedajúci konjugovanej hodnote cieľovej impedancie.
Prvá časť tohto článku bola venovaná popisu Smithovho diagramu, ktorý vďaka svojim vlastnostiam výrazne zjednodušuje návrh vysokofrekvenčných obvodov. Jeho praktické využitie bolo ukázané na príklade návrhu dvojprvkového úzkopásmového prispôsobovacieho obvodu, čo však predstavuje len nepatrnú časť jeho možného využitia. V ďalšej časti článku si bližšie rozoberieme širokopásmové prispôsobovacie obvody.
Ing. Milan Hammer vyštudoval Rádioelektroniku na FEI STU v Bratislave v roku 1997. Počas svojej vyše 15 ročnej praxe pracoval na inžinierskych pozíciách pre viaceré Hi-Tech spoločnosti zaoberajúce sa vývojom integrovaných obvodov a elektronických zariadení. Jeho hlavným zameraním je vývoj aktívnych a pasívnych obvodov vo vysokofrekvenčnej a mikrovlnnej oblasti ako aj riešenie problematiky Elektromagnetickej kompatibility. V súčasnosti pod svojou firmou Mil1 spolupracuje ako RF expert na projektoch domácich a zahraničných firiem. V prípade záujmu ho môžete kontaktovať na mil1@mil1.sk, alebo milan.hammer@gmail.com. Pre viac informácii, navštívte webovú stránku www.mil1.sk.
