Položení spojů na desku pomocí sběrnic

Dnes nejsou výjimkou desky plošných spojů (DPS) s více než 10 000 spoji a 14 signálovými vrstvami. Možnosti položení spojů (routování) jsou pak vzhledem k vysoké hustotě vývodů velmi omezené. Je zde velké množství spojů, které je třeba vyvést z hustých polí vývodů na okraj obrysu součástky a dále je propojit s ostatními součástkami. Úspěšné routování spojů je rozděleno do dvou částí – vyvedení spojů zpod součástek na jejich okraj (escape routing) a vzájemné propojení takto vyvedených spojů po celé desce (board/area routing). O metodě „escape routing“ jsem se zmínil v tomto časopisu již dvakrát, v tomto článku se tedy podíváme na položení zbývajících spojů mezi součástkami – „board/area routing“.

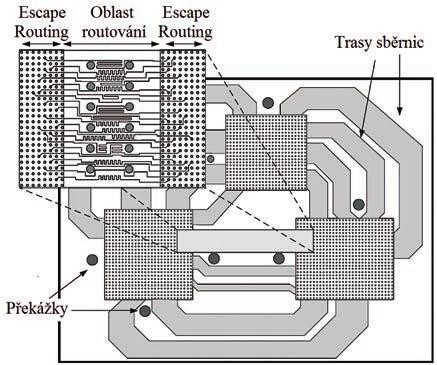
Obr. 1 Řešení návrhu desky pomocí sběrnic

Obr. 1 představuje řešení pomocí sběrnic spojů. V přiblíženém výřezu vlevo nahoře je symbolicky zobrazeno položení spojů pod součástkami pomocí escape routingu a jejich vzájemné propojení (area routing). Zbývající část obrázku naznačuje možné propojení součástek pomocí tzv. sběrnic spojů (bus, bundles atd.), kdy sběrnice představuje shluk plošných spojů, které jsou na desce vedeny spolu. U některých desek patří více jak 90 % spojů sběrnicím. Jsou pochopitelně situace, kdy některé spoje nelze zařadit do žádné sběrnice.

Z obrázku č. 1 je patrné, že navrhnout „rozumně“ takovou desku znamená optimalizovat několik věcí najednou. Především je vhodné po umístění součástek provést optimalizaci polohy zaměnitelných vývodů (pin swap) uvnitř jednotlivých součástek. Tento krok by měl přinést minimum křížení vzdušných spojů (což velmi usnadňuje propojovací proces) a také minimalizovat jejich celkové délky. Druhým optimalizačním krokem je definování sběrnic a jejich následná geometrická realizace. To je ve skutečnosti celá řada kroků, které nakonec vyústí v komplexní návrh složité desky. Samozřejmě je možné, že v některém kroku se zjistí, že úloha při daném rozmístění nebo rotaci součástek nemá řešení, anebo je řešení natolik nevyhovující, že je nutné provést nové rozmístění součástek a optimalizační kroky opakovat. Velkou výhodou použití automatizovaných přístupů je možnost realizace několika variant řešení v relativně krátké době a pak vybrat to nejlepší. Manuální přístup tuto variabilitu neumožňoval vzhledem k neúnosným časovým nárokům na takové zpracování. Další obsah tohoto článku se bude snažit o populární vysvětlení kroků, kterými se automatizované řešení zabývá. Algoritmy jsou většinou z dílny vývojářů University of Illinois v Urbana Champaign.

Posloupnost sběrnic spojů

Jak již bylo zmíněno výše, spoje jsou organizovány do sběrnic, přičemž je preferováno řešení, kdy sběrnice neobsahuje spoje, které do ní nepatří. Všechny doposud existující algoritmy jsou net-centrické, tzn., že jejich aplikace má za následek míchání různých spojů. Zde je uveden bus-centrický algoritmus, který pracuje se spoji jednotlivých sběrnic, rozdělený do dvou fází:

a) nalezení množiny sběrnic, které mohou být vedeny v téže vrstvě bez křížení,

b) realizace spojů uvnitř sběrnic algoritmem „escape routing“.

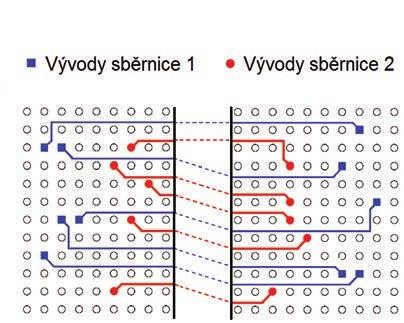
Obr. 2 Příklad propojení dvou součástek

Na obr. č. 2 je uveden případ dvou sběrnic, jejichž návrh je společný a kdy spoje obou sběrnic jsou smíchány dohromady – tedy nežádoucí stav. K řešení problému je zaveden pojem projekčního intervalu – viz obr. č. 3.

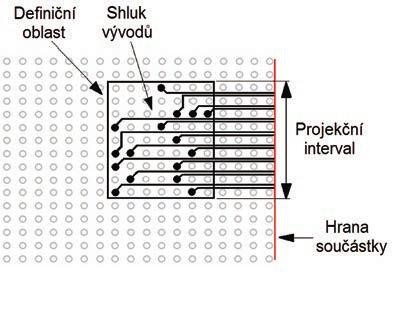
Obr. 3 Znázornění projekčního intervalu sběrnice na hranici součástky

Je zde znázorněn shluk vývodů sběrnice (Pin Cluster), obdélník obepínající všechny vývody sběrnice (Bounding Box) a projekční interval a jeho šířka na hranu součástky. Pokud projekční interval sestrojíme u všech sběrnic mezi 2 součástkami, dostaneme situaci znázorněnou obr. 4. Z obrázku je na první pohled evidentní, že řešení lze realizovat bez křížení a míchání spojů na dvou vrstvách, na jedné sběrnice A, D, E, na druhé vrstvě B a C.

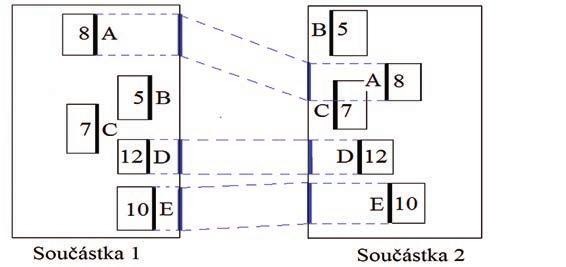
Obr. 4 Pět sběrnic A, B, C, D, E o šířkách (počtu spojů uvnitř) 8, 5, 7, 12 a 10 a jejich projekční intervaly

Obecný algoritmický přístup řeší maximální sumu šířek projekčních intervalů zúčastněných sběrnic na obou hranicích součástek, což je úloha dynamického programování. Držíme se požadavku návrháře desky na vedení spojů sběrnice pouze na jedné vrstvě. Pokud máme pro jednotlivé sběrnice přiřazeny vrstvy, můžeme přejít k otázce nalezení cest, které se nekříží, pro spoje v rámci sběrnice, jak je znázorněno na obr. 5.

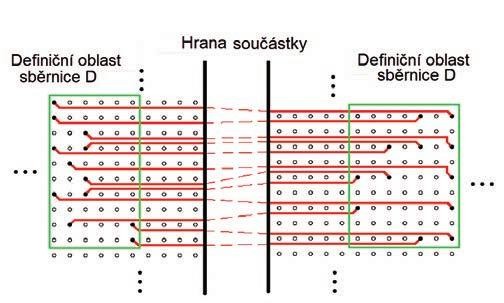
Obr. 5 Nekřížící se spoje ve sběrnici D (šířka 12)

Pokud trochu „oslabíme“ práci algoritmu, který pracuje přesně, můžeme pomocí projekčních intervalů najít suboptimální řešení, neboť výběr neprotínajících se projekčních intervalů u obou součástek je dobře vizuálně řešitelný. To odpovídá i intuitivnímu přístupu, který ve svých návrhových systémech preferují firmy Cadence (IFP) nebo Intercept, kde díl odpovědnosti za optimální řešení nese erudice návrháře.

Přiřazení vývodů (pin assignment)

U návrhů desky znamená přiřazení vývodů přiřazení signálu určitému vývodu součástky, přičemž uvažujeme maticové uspořádání vývodů. Vývody s přiřazeným stejným signálem budou později propojeny během procesu routování. Na přiřazení vývodů se můžeme také dívat jako na propojení vývodů dvou různých součástek. Je to velmi důležitý krok následující v návrhu desky hned po rozmístění součástek, neboť významně ovlivňuje výsledek routování. Některá přiřazení vedou k jednoduchým propojením, zatímco jiná vedou ke komplikovaným propojením (viz obr. 6).

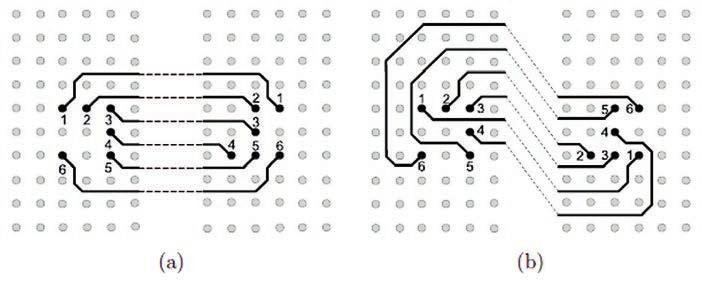
Obr. 6 Jednoduché a komplikovanější propojení vývodů v rámci dvou součástek

Optimálním přiřazením vývodů dosáhneme minimálního křížení vzdušných vodičů, což signalizuje snadnější budoucí propojení a také minimalizaci celkové délky budoucích spojů. V neposlední řadě se ideálně přiřazeným vývodům snadno přiřazuje sběrnice. Jen připomeňme velmi významný faktor ovlivňující propojitelnost i optimální provedení přiřazení vývodů – je to volná plocha použitelná pro vedení spojů mezi pájecími ploškami vývodů. Citlivé nastavení mezer a šířek tras může znamenat vedení dvou nebo i tří tras mezi vývody, což opět znamená obrovský posun směrem ke snadnějšímu propojení.

Plánování sběrnic spojů

Plánování sběrnic spojů zahrnuje přiřazení sběrnic jednotlivým vrstvám a topologické routování na těchto vrstvách v planární podobě (realizace bez použití průchodů mezi vrstvami). Tento úkol je jeden z časově nejnáročnějších kroků v návrhu desky a také jeden z nejsložitějších. Na obr. č. 7 je zobrazen výsledek plánování sběrnic na jedné vrstvě.

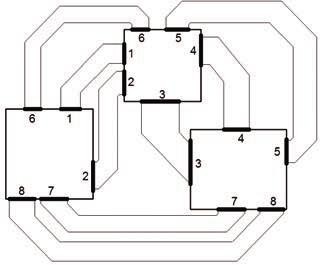
Obr. 7 Několik disjunktních sběrnic propojuje součástky na jedné vrstvě

Návrhy desek v praxi obsahují více takových vrstev. Během plánování sběrnic nesmí dojít k jejich křížení, přičemž je žádoucí minimalizace celkové délky spojů uvnitř zúčastněných sběrnic. Jak je známo, existující komerční nástroje používají k plánování sběrnic interaktivní přístupy. Zde je nutné připomenout značný rozdíl mezi globálním routováním a plánováním sběrnic. Zatímco globální routování používá X/Y dělení tras do vertikálních a horizontálních segmentů na různých vrstvách, u sběrnic je požadován návrh na jedné vrstvě, protože každý via otvor může ovlivnit spolehlivost a výkon obvodu, poškodit integritu signálu a zvýšit výrobní náklady. Tento fundamentální rozdíl neumožňuje tradičním autorouterům práci s těmito sběrnicemi. Vývojáři z Illinois byl vyvinut údajně první automatický „bus planner“ pro plánování sběrnic při komplexním návrhu desky. Jejich program pracuje ve třech etapách:

•  Globální routování pracující se sběrnicemi na jedné vrstvě.
•  Přiřazení vrstev navrženým sběrnicím.
•  Interaktivní vylepšení všech přiřazení a re-routing.

Tento nový algoritmus pro plánování sběrnic byl testován na průmyslových návrzích s více než 7 000 signály (nets) a 12 vrstvami, které byly předtím kompletně navrženy manuálně. Při 100% propojitelnosti potřeboval pro návrh sběrnic 40 minut při srovnatelné celkové délce spojů, zatímco manuální návrh zabral týdny.

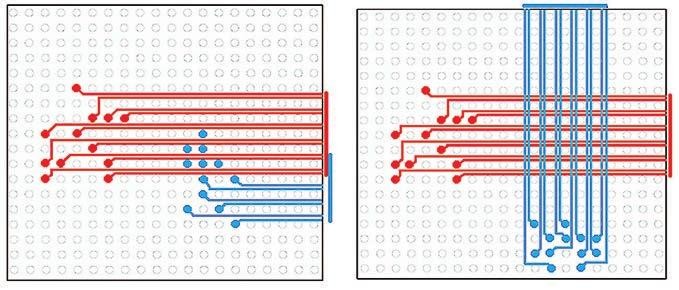
Obr. 8 Problematika plánování sběrnic, křížení a kolize projekčních intervalů

Na obr. č. 8 najde čtenář ilustraci základního problému s plánováním sběrnic spojů – vyvedení jednotlivých sběrnic na jedné vrstvě na okraj součástky bez křížení a kolize s ostatními busy. V jednom případě se sběrnice kříží (vpravo), ve druhém koliduje jejich projekční interval (vlevo).

Vstupními údaji do programu pro plánování sběrnic jsou počet vrstev určených k routování, množina projekčních intervalů busů a tzv. „conflict bus graph“ (obr. 9b – znázorňuje vazby mezi sběrnicemi, které jsou navzájem konfliktní).

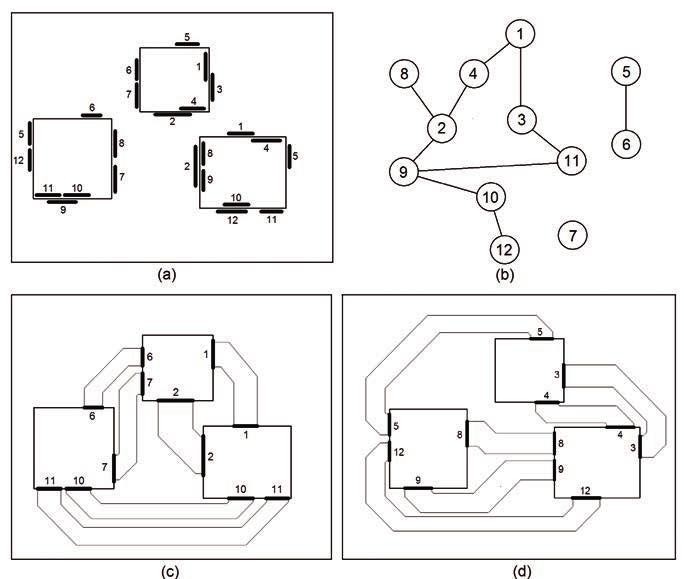
Obr. 9 Příklad řešení sběrnic – a) projekční intervaly sběrnic 1–12, b) graf konfliktů mezi sběrnicemi c), d) – řešení sběrnic na dvou vrstvách

Obr. 9a představuje počáteční situaci, kde je 12 sběrnic propojujících 3 součástky, přičemž všechny sběrnice mají vyvedeny na obrys součástek své projekční intervaly. Obr. 9b znázorňuje konflikty sběrnic (conflict bus graph), kde např. sběrnice 4 koliduje se sběrnicí 1 a 2 (protínají se projekční intervaly), sběrnice 9 koliduje se sběrnicemi 2, 10 a 11 atd. Obr. 9c a 9d ukazují, že zadání bylo možné řešit na dvou vrstvách.