Smithov diagram a prispôsobovacie obvody – časť 2
Úvod
V časti 1 tohto článku [1] sme si opísali metódu návrhu úzkopásmového dvojprvkového prispôsobovacieho obvodu. Jeho hlavnou výhodou je jeho jednoduchosť, avšak pri samotnom návrhu môžeme naraziť na viacero problémov. Výsledné hodnoty jednotlivých prvkov môžu byť príliš veľké alebo, naopak, malé. Pri sériovej výrobe nám môže v niektorých prípadoch prekážať veľká citlivosť na zmenu hodnôt súčiastok. Ďalšou nevýhodou tohto riešenia je malá flexibilita z hľadiska celkového návrhu aplikácie (ak chceme napríklad optimalizovať dizajn aj z pohľadu iných parametrov ako skreslenie, šírka pásma, výťažnosť atď.). Veľkú časť týchto nevýhod vieme eliminovať viacprvkovým zapojením prispôsobovacích obvodov, ktoré však už vieme použiť aj na širokopásmové prispôsobenie.
Návrh širokopásmového prispôsobenia
V predchádzajúcich častiach seriálu sme si ukázali, že na prenos maximálneho výkonu do záťaže potrebujeme navrhnúť bezstratový prispôsobovací obvod zložený z čisto reaktívnych prvkov (indukčnosti a kapacity), ktorý minimalizuje činiteľ odrazu | Γ |.
Kým návrh úzkopásmového prispôsobenia je pomerne jednoduchý, širokopásmové prispôsobenia má určité špecifiká, ktoré si opíšeme v tejto časti.
Hlavný rozdiel oproti úzkopásmovému obvodu je ten, že v prípade širokopásmového prispôsobenia vieme dosiahnuť ideálne prispôsobenie (| Γ | = 0) iba pre čisto rezistívne záťaže (jx = 0). Matematicky sa dá dokázať, že minimálna dosiahnuteľná hodnota činiteľa odrazu závisí od kvality komplexnej záťaže, počtu prvkov prispôsobovacieho obvodu a požadovanej šírky pásma, v ktorom chceme záťaž prispôsobiť k zdroju.
Kvalita komplexnej záťaže QLje tu definovaná ako pomer jej imaginárnej a reálnej časti a vypočítame ju zo vzťahu QL= X/R v prípade sériovej náhradnej schémy, resp. QL= B/G v prípade paralelnej náhradnej schémy záťaže. Na obr. 1 sú zobrazené základné typy komplexnej záťaže so vzťahmi pre výpočet ich kvality. Hodnota f0tu predstavuje strednú hodnotu frekvenčného pásma
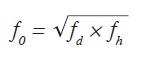
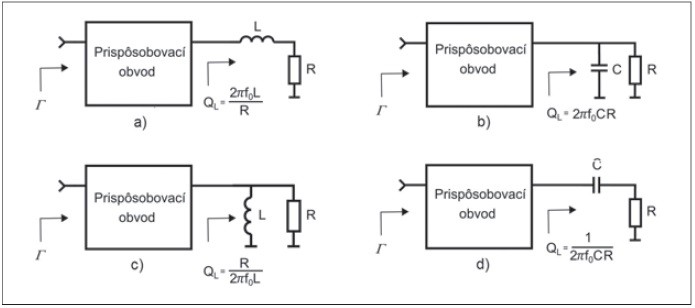
Obr. 1 Zobrazenie kvality záťaže QL pre štyri základné typy záťaže ZL
Teraz, keď vieme, že ideálne prispôsobenie pre ľubovoľnú šírku pásma nie je možné dosiahnuť pre záťaže s nenulovou hodnotou kvality, bolo by dobré aspoň zistiť nejaký dosiahnuteľný limit, ku ktorému sa pri dodržaní určitých zásad vieme dopracovať.
Tento limit je daný Fanovým integrálom, ktorý nám určuje kompromis medzi šírkou pásma a dosiahnuteľnou kvalitou prispôsobenia.
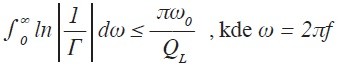
Fanov integrál rieši situáciu zobrazenú na obrázku 2. Predpokladáme tu modelový stav, keď činiteľ odrazu má určitú konštantnú hodnotu | Γ |min(resp. | Γ` |min) v celom požadovanom frekvenčnom pásme od fdpo fh(resp. od f`dpo f`h) a pre všetky ostatné frekvencie je | Γ | = 1.
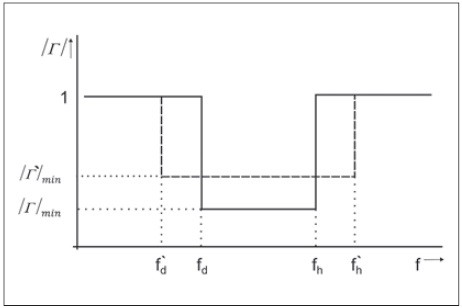
Obr. 2 Kompromis medzi šírkou pásma a dosiahnuteľným prispôsobením
Riešením tohto integrálu je rovnica udávajúca teoretickú minimálnu hodnotu činiteľa odrazu v závislosti od šírky pásma a komplexnej impedancie pri použití prispôsobovacieho obvodu tvoreného nekonečným počtom ideálnych prvkov
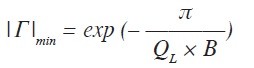
kde QLje kvalita záťaže podľa obr. 1 a B je normovaná šírka pásma
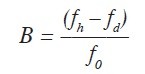
Z rovnice vyplýva, že čím väčšiu šírku pásma požadujeme, tým väčšiu hodnotu činiteľa odrazu musíme akceptovať. A rovnako môžeme písať, že čím má prispôsobovaná záťaž vyššiu kvalitu, tým bude návrh prispôsobenia náročnejší a pravdepodobne sa budeme musieť uspokojiť s horším výsledkom.
Opäť nám ako dobrá pomôcka pri samotnom návrhu prispôsobovacieho obvodu poslúži Smithov diagram, do ktorého si môžeme zakresliť krivky konštantnej kvality. Tieto krivky sú jednoducho utvorené pospájaním bodov zobrazujúcich impedancie s rovnakým pomerom imaginárnej a reálnej časti (obr. 3).
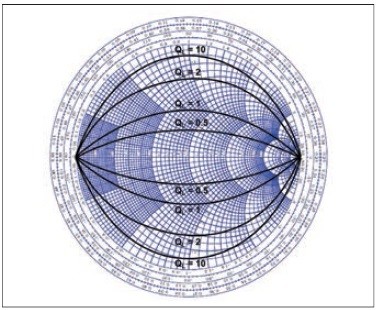
Obr. 3 Smithov diagram so zobrazením kriviek konštantnej kvality
Využitie tejto pomôcky pri konkrétnom návrhu viacprvkového prispôsobovacieho obvodu si názorne ukážeme na nasledujúcom príklade.
Závislosť šírky pásma od dráhy prispôsobenia
Závislosť šírky pásma od dráhy prispôsobenia si ukážeme na príklade, v ktorom bude našou úlohou navrhnúť trojprvkový prispôsobovací obvod na prispôsobenie komplexnej impedancie, tvorenej sériovou kombináciou rezistora R = 100 Ω a indukčnosti L = 100 nH (podľa obrázka 1a) k impedancii zdroja Z0= 50 Ω vo frekvenčnom pásme so stredom f0= 433 MHz.
Na rozdiel od dvojprvkového prispôsobovacieho obvodu opísaného v prvej časti článku, pri návrhu viacprvkových prispôsobovacích obvodov máme oveľa väčší stupeň voľnosti, a tak riešení danej úlohy môže byť viac. Z nich som vybral 2 zapojenia (obrázok 4 a, b), na ktorých bude vidno, ako závisí výsledná šírka pásma prispôsobenia od navrhnutej dráhy prispôsobenia. Návrh je opäť simulovaný pomocou softvéru RFSim99, ktorý je voľne šíriteľný a dá sa jednoducho nájsť a stiahnuť z internetu.
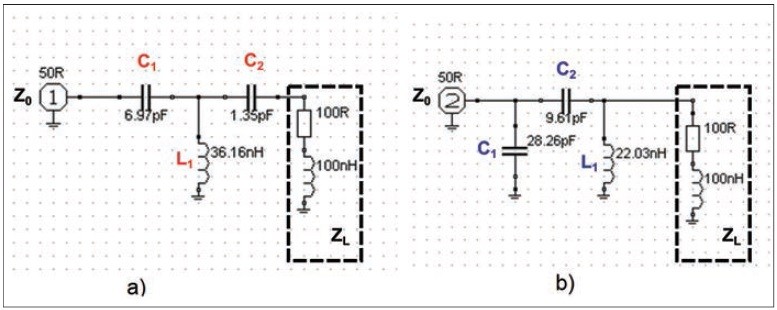
Obr. 4 Schémy zapojenia prispôsobovacích obvodov
Postup pri návrhu obvodu na obrázku 4a) je znázornený na obrázku 5 červenou krivkou, postup pri návrhu obvodu na obrázku 4b) modrou krivkou. Bod ZLna Smithovom diagrame zobrazuje prispôsobovanú záťaž pri strednej frekvencii f0= 433 MHz, čiarkované čiary znázorňujú pohyb po kružnici konštantnej admitancie (paralelné pripojenie prvku) a plné čiary pohyb po kružnici konštantnej impedancie (sériové pripojenie prvku). Vidíme, že v oboch prípadoch sme sa pomocou troch reaktívnych prvkov dostali pri strednej frekvencii do stredu Smithovho diagramu, ktorý predstavuje impedanciu Z0. Rovnako je však zjavné, že pri prvom riešení (červená krivka) je prispôsobovacia dráha oveľa kratšia a zároveň sa pohybujeme bližšie k stredu diagramu. Naopak, pri druhom riešení je dráha krivky dlhšia a prechádza oblasťou s väčšou kvalitou impedancie. Toto všetko má za následok, že prispôsobovací obvod na obrázku 4a) je podstatne širokopásmovejší, čo vidíme aj z porovnania na obrázku 6. Na základe tohto príkladu môžeme napísať pravidlo, že pri návrhu širokopásmového obvodu pomocou Smithového diagramu by sme sa mali snažiť dosiahnuť čo najkratšiu dráhu od prispôsobovanej záťaže do stredu diagramu. Rovnako by sme sa mali snažiť udržať dráhu čo najďalej od okrajov diagramu a čo najbližšie k reálnej osi.
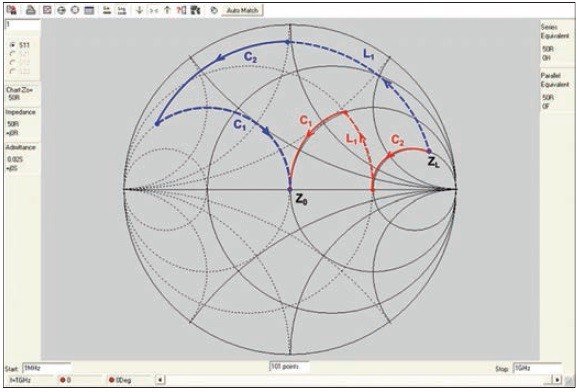
Obr. 5 Grafické znázornenie návrhu prispôsobovacích obvodov
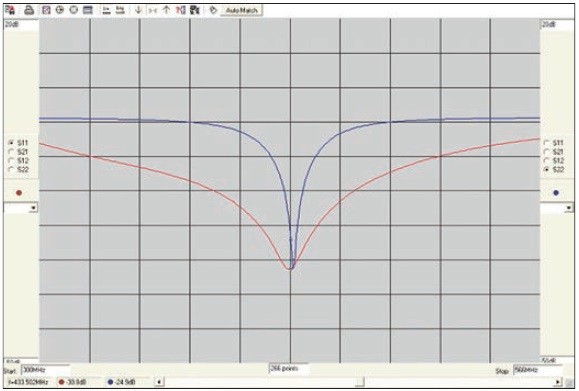 a obr. 4b (modrá krivka).jpg)
Obr. 6 Porovnanie šírky pásma prispôsobovacích obvodov podľa obr. 4a (červená krivka) a obr. 4b (modrá krivka)
Závislosť šírky pásma od počtu prvkov prispôsobovacieho obvodu
Pri pohľade na obr. 5 vieme usúdiť, že použitím viacerých prvkov by sme vedeli navrhnúť ešte kratšiu dráhu a tým dosiahnuť väčšiu šírku pásma pri rovnakej kvalite prispôsobenia. Na dokázanie tejto úvahy som navrhol prispôsobovacie obvody zložené z 2, 3, 4 a 12 prvkov. Komplexnú záťaž, ako aj strednú frekvenciu som použil rovnakú ako v príklade 1. Výsledky simulácií sú znázornené na obrázku 7, ktorý dokazuje, že maximálne dosiahnuteľná šírka pásma závisí aj od počtu použitých prvkov.
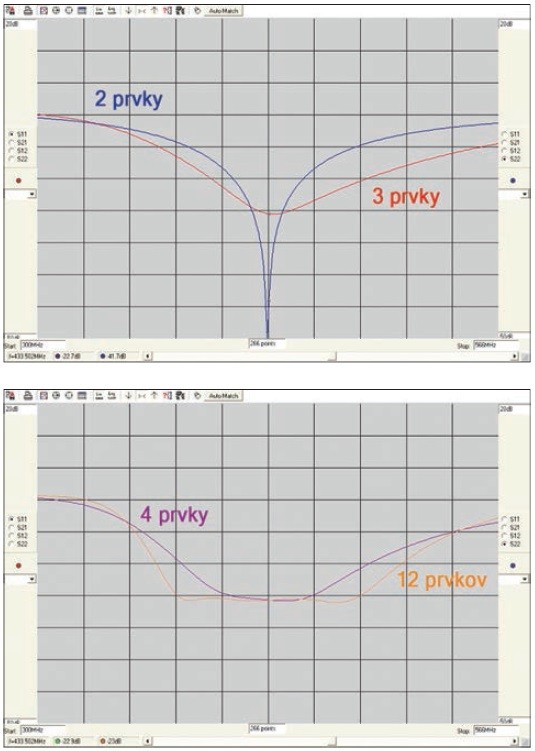
Obr. 7 Porovnanie dosiahnuteľnej šírky pásma v závislosti od počtu prvkov prispôsobovacieho obvodu.
Záver
Na základe uvedenej teórie a príkladov môžeme napísať niekoľko zásad využiteľných pri praktickom návrhu širokopásmových prispôsobovacích obvodov.
Maximálna dosiahnuteľná šírka pásma závisí od kvality záťaže, preto pri návrhu volíme na Smithovom diagrame dráhu prispôsobenia tak, aby sme sa pohybovali v pásmach s čo najmenšou kvalitou. Inými slovami, vyhýbame sa okrajom Smithovho diagramu a snažíme sa voliť dráhu čo najbližšie k reálnej osi diagramu.
Pri prispôsobení sa snažíme, aby bola dráha prispôsobenia čo najkratšia. Ak pri návrhu zistíme, že s daným počtom prvkov nevieme dosiahnuť požadovanú šírku, skúsime zvýšiť počet prvkov prispôsobovacieho obvodu. Musíme však stále počítať s tým, že aj keby sme mali prispôsobovací obvod s nekonečným počtom prvkov, maximálne dosiahnuteľná šírka pásma pre danú komplexnú záťaž a požadovaný činiteľ odrazu je limitovaná Fanovým integrálom.
V tretej, záverečnej časti článku sa budem venovať návrhu širokopásmových prispôsobovacích obvodov s využitím impedančných transformátorov.
Literatura
[1] DPS Elektronika od A do Z, č. 4/2013
[2] HF Radio Systems & Circuits – William E. Sabin, Edgar O. Schoenike, 1998, Noble Publishing Corporation
[3] R. C. Hansen, „Correct Impedance-Matching Limitations,“ IEEE Antennas and Propagation Magazine, 51, 3, June 2009, pp. 122124.
[4] R. M. Fano, „Theoretical Limitations of the Broadband Matching of Arbitrary Impedances,“ J. Franklin Institute, 249, 1, January 1950, pp. 57–83; February 1950, pp. 139–154.




