BonnTools – matematické inovace algoritmů používaných při návrhu čipu

Abychom stále neinformovali jen o novinkách v oblasti návrhu DPS a čipů pocházejících z anglosaské půdy, podívejme se nyní na práci německých matematiků a vývojářů. Výsledek jejich práce nese název BonnTools.

BonnTools je více než 20 let vyvíjený a stále zdokonalovaný systém automatizovaných nástrojů (rozmístění, autorouting, …) určený pro návrh složitých DPS a čipů. Za dobu své existence neustále reaguje na potřeby návrhářů. Je společným dílem matematiků bonnské university a inženýrů německé pobočky IBM. Pokud se při vývoji čipu vyskytne nový problém, nastává práce na nových přístupech a algoritmech, které problém řeší. Zde má hlavní slovo matematika. To samo o sobě dává tušit, že jde o nástroj velmi vysoké kvality z algoritmického pohledu, který ale nemá jen teoretický dopad, protože vyvinuté algoritmy vyhovují skutečným potřebám praxe.

V článku přiblížíme vždy zadání úlohy a cíl, kterého má daný nástroj dosáhnout. Samotný matematický slovník popisující algoritmy se pokusíme zjednodušit na úroveň srozumitelnou čtenáři. Pokud mluvíme o nástrojích, rozumíme tím realizaci rozmístění součástek (bloků) na čipu nebo DPS – tato procedura v rámci BonnTools nese název BonnPlace. Úlohu routování řeší část programu nazvaná BonnRoute.

Obrovský rozvoj VLSI technologie, hojnost zajímavých a jasně definovatelných optimalizačních problémů vznikajících v různých konstrukčních krocích návrhu a hospodářský význam učinily z VLSI designu jednu z nejzajímavějších aplikací diskrétní matematiky. Od roku 1987 bylo navrženo přes 1 000 čipů pomocí BonnTools. Ty obsahují kompletní řešení pro rozmístění a routování a další nástroje nutné při vývoji čipu. BoonTools jsou používány v mnoha návrhových centrech po celém světě. Pojďme nyní přiblížit práci jednotlivých procedur matematickým pohledem.

Rozmístění (Placement)

Cílem rozmístění je optimální vzájemná poloha všech bloků na čipu zaručující následné bezproblémové propojení mezi bloky vodivými cestami. V této proceduře dochází k minimalizaci celkové délky budoucích spojů, definici kanálů mezi bloky s dostatečnou kapacitou pro vedení tras, důležitá je i rovnoměrná hustota budoucích vodičů na podložce. Bonn- Place, který úlohu rozmístění řeší, obsahuje algoritmy pro globální a detailní rozmístění. Globální rozmístění umísťuje bloky do optimálních pozic z hlediska vzájemných vazeb, jejich počtu a důležitosti. Umístěné bloky mají ale přesahy svých obvodových pravoúhelníků, které jsou odstraňovány v dalším kroku, v detailním rozmístění. Detailní rozmístění má globální umístění jako vstup a realizují se zde pouze lokální změny.

Globální rozmístění má dvě hlavní složky: kvadratické rozmístění a část zvanou „multisection“. V každé fázi globálního rozmístění je plocha čipu dělena na regiony a každému regionu je přiřazen posouvatelný blok. Vznikají tak dílčí oblasti (subregiony) a bloky se posouvají do nových pozic až do jejich „rozprostření“ po oblasti čipu s možností minimálních přesahů jejich obrysů. Po konečném dělení oblasti čipu počet řádků takto vzniklé matice odpovídá počtu řádků čipu, každý o velikosti standardní buňky, počet sloupců je menší a každý z nich obsahuje několik desítek posouvatelných bloků. Toto je počáteční situace, do níž vstupuje optimalizační proces. Pro představu, čip v 65nm technologii obsahuje 5 000 řádků a kolem 1 000 sloupců. Kvadratické rozmístění řeší minimalizaci váhové funkce, která popisuje vzniklou geometrii bloků a jejímiž parametry jsou:

W – váhový koeficient každého spoje, kde je možné každému spoji přisoudit jakousi důležitost nebo ji naopak potlačit

N – počet pinů každého spoje

Xp,q – kvadrát X vzdálenosti pinů p a q téhož spoje v závislosti na tom, zda piny p a q jsou součástí fixních nebo posouvatelných bloků v rámci geometrie sloupců

Yp,q – kvadrát Y vzdálenosti pinů p a q téhož spoje, totéž jako u Xp,q s tím, že se uvažuje geometrie řádků

Kvadrát vzdáleností je zde proto, aby se posílila skutečnost, že bloky patří do jiného sloupce (řádku), což ovlivňuje budoucí křížení vodičů. Ve funkci je používán podíl W/(|N|-1), což je váhový koeficient podělený počtem pinů spoje. Ten má za úkol eliminovat dominanci spojů s velkým počtem pinů, které se velmi významně podílejí na hodnotě váhové funkce. Existuje několik důvodů pro optimalizaci této kvadratické váhové funkce. Za prvé zpoždění cest roste kvadraticky s délkou. Za druhé kvadratické rozmístění přináší optimální pozici posouvatelných bloků. Za třetí řešení pomocí kvadratického rozmístění je stabilní, tj. téměř neměnné při malých změnách v netlistu, kdy není nutné opakování rozmísťovací procedury. Konečně procedura minimalizace takto definované funkce je velmi dobře a rychle výpočtově realizovatelná.

Přejděme nyní k dílčí oblasti (multisection). Kvadratické rozmístění má obvykle mnoho překrytí bloků, které je nutno odstranit a k tomu účelu slouží právě tyto „multisection“. Tady je cílem s bloky posouvat co nejméně, ale tak, aby se navzájem nepřekrývaly. Tato úloha byla původně řešena Hitchcockovým transportním problémem, ale pro extrémní výpočetní čas byl tento algoritmus nahrazen vlastním heuristickým algoritmem s požadovaným výsledkem a v extrémně krátkém výpočetním čase. Bohužel tento algoritmus není v dokumentované práci dostatečně přiblížen, takže ho jen zmiňuji. Výsledkem globálního rozmístění je mapa nepřekrývajících se bloků na čipu. Rozmístění ale ještě není kompletní, protože je zde další optimalizační krok, kterým je detailní rozmístění.

Poznámka: Hitchcockův transportní problém popisuje úlohu, kdy je dáno C1, C2, …, Cn posouvatelných bloků s jejich velikostmi a1, a2, …, an a dále k regionů R1, R2, …, Rk s kapacitami b1, b2, …, bk, kde k <= n. Řeší se přiřazení C × R, v němž platí, že bloky přiřazené do určitého regionu součtem svých velikostí nepřesáhnou kapacitu regionu a pokud d(i,j) vyjadřuje cenu za posunutí bloku Ci do regionu Rj, hledá se minimum součtu takových cen. Výsledkem je disjunktní množina bloků v každém obsazeném regionu – tedy bloky se už nepřekrývají.

Detailní rozmístění

Detailní rozmístění se týká pohybu a fixace pouze standardních buněk, ostatní bloky jsou fixovány z globálního rozmístění. Cílem je pouze doladit pozici standardních buněk bez velké změny vstupního rozmístění. Jestliže v globálním rozmístění bylo dosaženo optimální rozmístění bloků s překryvy, algoritmus „multisection“ procedury tyto překryvy odstranil. Zde už jde jen o posunutí buněk do pozic v rámci volného prostoru a snahu kolem každého bloku vytvořit dostatečný prostor pro vedení spojů.

Routing

Globální autorouter pracuje na trojrozměrném modelu rastru, který se získává – jako obvykle – na základě rozdělení oblasti čipu do regionů. Pro klasický Manhattan routing (směry vodičů pouze vertikální a horizontální) je vytvořena paralelní síť s oběma směry, třetím rozměrem v tomto modelu jsou vrstvy. Regiony jsou vrcholy grafu globálního routingu a jsou spojeny se sousedním regionem hranou spolu se stanovením její kapacity. Ta určuje, kolik paralelních vodivých cest může mezi regiony vést. Takto ohodnocený graf je základem pro stanovení, kudy vést budoucí spoje tak, aby byl splněn požadavek na propojitelnost čipu v kterémkoliv místě. Vodivé cesty (v tomto případě ještě vzdušné spoje) jsou v podstatě spojnicí dvou pinů téhož spoje (spoj s více piny je dekomponován do spojnic dvou pinů), soustava všech spojek spojujících piny jednoho spoje se nazývá Steinerův strom. Kvalita globálního routingu závisí do značné míry na tom, jak se podaří sestrojit navzájem disjunktní Steinerovy stromy všech spojů tak, aby jejich promítnutí do kapacit grafu splňovalo propustnost hran grafu. Většinou se hledá minimální Steinerův strom, tj. sumární délka všech spojnic pinů (s pomocí Steinerových tzv. bodů) ve spoji je minimální. V tomto modelu se ale preferuje nalezení takového Steinerova stromu pro každý spoj, který neprotíná (nepřekáží, je disjunktní) stromy ostatních spojů. Při výpočtu velmi pomáhá existence více vrstev.

Detailní routing

Úkolem detailního routingu je určit přesné rozložení kovových realizací spojů. Je zde nutná efektivní struktura údajů, která uchovává pouze nejnutnější informace o tvarech spojů a umožňuje rychlé vyhledávání při realizaci mnohamilionových testů. Grid autorouteru definuje směr vodičů (a minimální izolační vzdálenost mezi trasami) a pracuje se s neúplným trojrozměrným grafem V(G) _ {xmin, … , xmax} × × {ymin, ... , ymax} × {1, . . . , zmax}, kde ((x, y, z), (x0, y0, z0)) je částí E(G) pouze, když |x − x0| + |y − y0| + |z − z0| = 1, jinými slovy, z jedné buňky rastru mohu přejít do sousední v horizontálním nebo vertikálním směru anebo změnit vrstvu, tj. přejít do sousední vrstvy. V(G) představuje v tomto zápisu trojrozměrnou mřížku, E(G) pak hranu mezi dvěma vrcholy grafu. Obvyklý počet vrstev čipu je 10. V tomto modelu se nemusíme starat o návrhová pravidla, jsou dána přímo mřížkou a v této etapě stačí topologický model, geometrický přijde na řadu později při přiřazování velikosti gridu ve vertikálním a horizontálním směru.

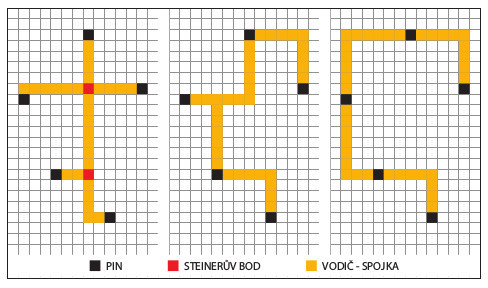
Obr. 1 Různé tvary Steinerova stromu pro spoj s více piny

Pro představu čtenáře má výše definovaný graf kolem 1011 vrcholů. Najít milióny disjunktních Steinerových stromů v tak obrovském grafu je velmi náročné. Proto je zvolena cesta dekompozice každého spoje do dvoubodových spojení, které tvoří Steinerův strom. Pak nastává elementární algoritmický úkol, totiž určit nejkratší cesty v detailním routingu v modelu grafu za použití výsledků globálního routingu.

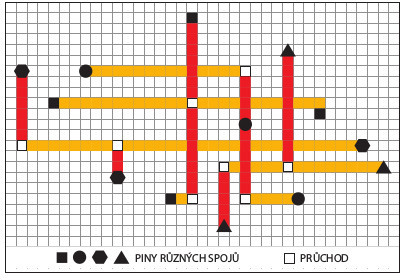
Obr. 2 Neprotínající se Steinerovy stromy: situace se 4 spoji

Výpočet nejkratších cest je pravděpodobně nejzákladnější a dobře nastudovaný algoritmický problém diskrétní matematiky, ale při velikosti grafu G a počtu nejkratších cest je jejich simultánní hledání nemožné. Proto jsou použity metody postupného hledání. Nejznámější je Dijkstra algoritmus. Jeho nejrychlejší verze za použití Fibbonacciho hromad běží v O (m + n log n) času, kde n a m značí počet vrcholů a hran. Z uvedeného počtu vrcholů grafu 1011 a počtu vrstev 10 vyplývá, že n a m jsou čísla řádově kolem 100 000. Pro tak velký graf je tato modifikace Dijkstra algoritmu příliš pomalá. Proto je v BonnRoute uplatněna strategie pro jeho urychlení. Vzhledem k tomu, že se nehledá jen jedna cesta, ale miliony disjunktních Steinerových stromů, jsou informace poskytnuté v globálním routingu velmi důležité. Pro každé dvoubodové spojení totiž globální routing určuje koridor a detailní routing skládá segmenty trasy v síti hran, která mu byla přidělena v globálním routingu. Pokud se najde nejkratší cesta dvoubodového spojení v rámci tohoto koridoru, odhady kapacit hran během globálního routingu přibližně zaručují nalezení všech disjunktních tras. Dalším efektem je dramatické zrychlení výpočtu, vzhledem k omezení vyhledávacího prostoru pouze na určený koridor a zmíněná velikost grafu už tolik nestraší.

Druhým významným faktorem urychlení hledání nejkratší cesty je způsob, jakým se ukládají informace o vzdálenostech. Vzdálenost vrcholů se snižuje nebo zvyšuje o jednu při přechodu z vrcholu na vrchol a pak je nutné uložit informaci jen pro jeden vrchol a přírůstek směru. Tato verze algoritmu Dijkstra označuje intervaly místo vrcholů a jeho časová složitost je tedy závislá na počtu intervalů, kterých je obvykle asi 100krát méně než počet vrcholů. Sofistikované datové struktury pro ukládání intervalů a odpovědi na dotazy algoritmu jsou velmi rychlé.

Závěrem je třeba uvést, že použití detailního routovacího grafu není omezeno pouze na grid-based routing. Nezáleží na tom, zda je budoucím trasám přidělen předdefinovaný směr, datová struktura je připravena i pro použití gridless routingu (hledání spojových cest bez použití gridu) s mírným zvýšením časové režie pro silnější trasy. Implementace algoritmu Dijkstra není ovlivněna použitým bezrastrovým přístupem k vedení cest. Ještě zmíníme rozdíl mezi grid modelem a gridless modelem prostoru při hledání vodivých cest. Grid model pracuje s pravidelnou mřížkou – viz text v tomto odstavci o detailním routingu. Je vhodný pro vodiče o stejné šířce a stejné izolační vzdálenosti, stačí pak nastavit vzájemnou relaci velikosti gridu, šířky a mezery a návrhová pravidla je snadné uhlídat. Pokud je na čipu nebo DPS použito více vodičů o různé šířce a izolačních vzdálenostech, a to je velmi častý případ dnešních návrhů, gridový model selhává. Nastupuje pak gridless model, který nové požadavky na různé šířky a mezery bere v úvahu. Přístupů ke gridless routingu je celá řada, od tzv. dlaždicového přístupu k hledání tras až k non-uniformním grafům, což je v podstatě také model mřížky, ale s proměnlivou velikostí gridu v každé z os x nebo y a také v každém místě na ose x nebo y. V tomto smyslu se podobá popsaný model gridovému a pak je možné použít vyvinuté datové struktury bez větších modifikací.

Jak bylo v úvodu zmíněno, řešení optimalizačních úloh je pro diskrétní matematiku v této oblasti velkou výzvou, málokdy má matematika takovou možnost uplatnit svůj potenciál v praxi, ale v uváděném případě to platí několikanásobně.