V současné době s použitím bezolovnatých pájek nabývá stále většího významu zkoumání spolehlivosti pájených spojů. O bezolovnatých spojích máme stále málo informací, proto setrvává nedůvěra na jejich používání. Spolehlivost pájeného spoje výrazně ovlivňuje nepřítomnost olova, které právě u olovnatých pájek snižuje křehkost spojení.
Článek popisuje dominantní mechanismy, které výrazně ovlivňují spolehlivost, přehledově uvádí základní teorii určování spolehlivosti a uvádí praktické zásady pro montáž. V článku je uvedena celá řada odkazů na literaturu, která se zabývá touto tematikou.
V případech nepružného pájeného spojení v elektrotechnice, za které je možno považovat pájení povrchově montovaných součástek SMD, je celý systém, včetně pájeného spoje střídavě mechanicky namáhán na tlak a tah v závislosti na teplotě. Změna teploty je způsobena buď při výrobě desky při pájení, nebo při provozu zařízení. Příčinou namáhání při změně teploty jsou různé hodnoty koeficientu délkové roztažnosti CTE (ppm/°C) jednotlivých materiálů sestavy. V tabulce 1 jsou uvedeny hodnoty CTE pro vybrané materiály, na obrázku 1 je uvedeno namáhání spoje v důsledku změny teplot.
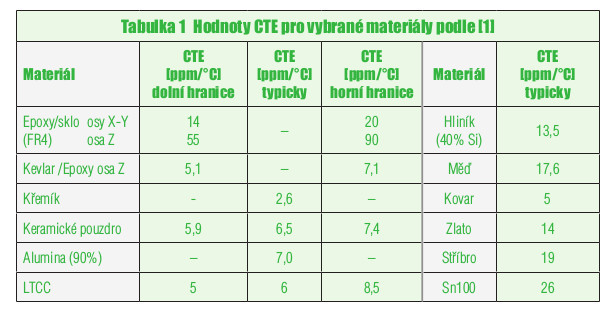
Tabulka 1 Hodnoty CTE pro vybrané materiály podle [1]
Za nepružné spojení je možno považovat spojení součástek nebo modulů uvedené na obrázku 2a, b. Pokud jsou části nepružně spojeny (může se jednat o pájku, vodivé lepidlo), vyvolává změna rozměru ε v relativně nepružném spojení změnu pnutí σ.
Obr. 1 Princip termomechanického namáhání
Velikost namáhání pro dané aplikace vyjadřují vztahy 1 a 2. Vztah 1 je Hookův zákon, který platí pro oblast pružných změn. Změna velikosti namáhání σe je úměrná změně velikosti poměrného posunutí Δεe a materiálové konstantě E (Youngův modul pružnosti).
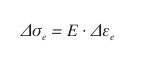
(1)
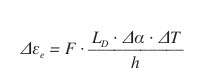
(2)
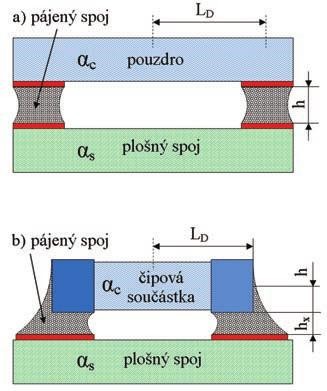
Obr. 2 Geometrie bezvývodového spojení
Mechanické chování měkkých pájek, které jsou používány v elektronice, vyjadřují diagramy uvedené na obrázku 3a, b.
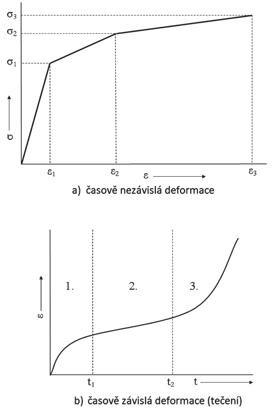
Obr. 3 Chování pájek při mechanickém zatížení
Hodnota poměrného posunutí ε (shear strain) vyvolává ve struktuře pájeného spoje materiálové pnutí σ. Do určitých hodnot namáhání, v grafu jsou to hodnoty σ1, ε1, je tato závislost lineární a jedná se o vratné pružné změny, které charakterizuje teplotně závislý Youngův modul pružnosti E. Pokud překročíme mez pružnosti (hodnoty σ1, ε1), začne se projevovat nepružná deformace, v první fázi jako počáteční plastická deformace, která postupně přechází od σ2, ε2 do oblasti saturace (σ3, ε3) a dále.
V této oblasti trvalé deformace, které nastanou po ukončení zatížení, jsou považovány za nepružné a mohou být časově nezávislé, nebo časově závislé (tečení materiálu).
Časově závislá deformace je znázorněna na obrázku 3b. V počáteční fázi 1. dochází výrazně ke snížení pnutí, ve fázi 2. dochází k ustálení.
V posledním stadiu 3. se zatížení prudce snižuje a konečným výsledkem je přerušení spoje. Nepružné deformace jsou vždy doprovázeny trvalými změnami v materiálu, hlavně posuny částic ve struktuře materiálu. Z hlediska spolehlivosti pájených spojů hrají hlavní roli změny v oblasti plastických deformací.
Výzkum plastických mechanických vlastností v oblasti pájených spojů se v současné době soustřeďuje na oblast bezolovnatých pájek, převážně binárních nebo ternárních slitin Sn-Cu, nebo Sn-Cu-Ag. Pro tuto oblast je zpracována a používá se celá řada matematických modelů, jako je Norton, Double Power Law, Garofallo [4], Anand [5], [6] a ostatní. Podrobný popis modelů včetně materiálových konstant pro bezolovnaté pájky je uveden v [7], [8], [9].
Pro stanovení spolehlivosti se používají zrychlené testy. V tomto případě je pájený spoj vystaven teplotním cyklům definované amplitudy a frekvence. Počet cyklů do poruchy je závislý na velikosti zatěžování. Poruchy způsobené termomechanickým namáháním patří do skupiny tzv. „nízkocyklové únavy“ (Low Cycle Fatique). V tomto případě se zkoumá chování spoje při nízkých frekvencích a vysokých amplitudách, kdy jsou dominantní mechanismy tečení materiálu, často až do zničení spoje.
Během cyklování je třeba vyhodnocovat mechanické, a hlavně elektrické vlastnosti spojení. Pro potřeby elektroniky je stěžejní vyhodnotit elektrické vlastnosti spojené se stálým nebo časově závislým přerušením spoje. Velice důležité je také znát závislost spolehlivosti na povrchové úpravě a tvaru pájených ploch.
Na základě experimentů uvedených v [2] bylo zjištěno, že defekty v pájeném spoji způsobené termomechanickým namáháním mají v konečném efektu charakter elektrického přerušení, jehož délka se pohybuje od μs do jednotek sekund v závislosti na počtu cyklů a momentální teplotě při cyklování.
Pro předpovídání termomechanické spolehlivosti se v praxi využívá celá řada matematických modelů, které vycházejí ze změny hustoty vnitřní energie při elasticko- plastické deformaci spoje. Základním vztahem je Morrow rovnice,
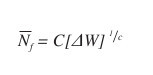
(3)
kde Nf je počet cyklů do poruchy, C a c jsou konstanty, ΔW je celková změna elasticko-plastické energie při jednom teplotním cyklu. Z této rovnice je možno odvodit velice často používaný Coffin- -Mansonův vztah,
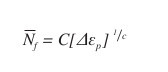
(4)
kde Δεp je cyklicky aplikovaná plastická změna (poměrné posunutí), C a c jsou materiálové konstanty.
Poměrně vyčerpávající teorie popisované tematiky, rozdělení elektroniky do kategorií podle oblasti používání spolu s doporučeními na měření je uvedeno v [1], [2].
 |  |
Obr. 4 Porucha způsobená termomechanickým namáháním, čipová součástka 2512, 6000 teplotních cyklů –20 až 100 °C, povrchová úprava HAL [2]
Na obrázcích 4 a 5 jsou uvedeny příklady závad, které se mohou vyskytnout při nepružném připájení.

Obr. 5 Prasklina na keramickém kondenzátoru [10]
a) doporučuje se spojovat materiály, které mají stejnou nebo aspoň podobnou délkovou roztažnost. Konkrétně pro součástky v keramickém pouzdře se doporučuje pro pájení na klasický materiál FR4 maximální vzdálenost nejvzdálenějších kontaktů 5 mm (2LD). Toto splňují téměř všechna čipová pouzdra,
b) v [11] jsou uvedena měření, kdy byla použita keramická podložka z keramiky (Aluminy) připájená na FR4 při vzdálenosti spojů 2LD = 21 mm nepružným hranovým připojením podle obr. 2b při tepelném namáhání 0 až 100 °C. První porucha (prasklina) se projevila při 800 teplotních cyklech. Z toho se dá předpokládat, že při připájení podobně velikého keramického BGA pouzdra na organický materiál FR4 nebude termomechanická spolehlivost výrazně vyšší než 1000 teplotních cyklů,
c) pro pájení rozměrnějších modulů (GPS a další) je třeba, aby byl modul zhotoven na stejném podkladě, jako je plošný spoj (nejčastěji FR4),
d) obecně se pružnost pájeného spoje zvyšuje s jeho pájecí výškou. Je třeba volit takovou konstrukci, aby výška byla co největší, konkrétně při kuličkovém spojení co největší průměr kuliček, případně zvolit některou z variant připojení popsaného v [2].
[1] IPC-SM-785, Guidelines for Accelerated Reliability Testing of Surface Mount Solder Attachments, průmyslová norma 1992
[2] Josef Šandera, Technologie a spolehlivost pájeného připojení elektronických modulů a součástek pro povrchovou montáž, FEKT, VUT Brno, habilitační práce, Brno 2010
[3] Engelmaier, W., (2009), Solder joint reliability prediction for chip components, MELFs,TSOPs, SOTs, Global SMT and Packaging. Vol. 9. no. 7
[4] Dongkai Shangguan, Lead-Free Solder Interconnect Reliability, ASM International, Materials Park, OH 44073-0002, August 2005
[5] NING Bai, Xu Chen, Hong Gao, Simulation of unaxial tensile properties for lead-free solders with modified Anand model, Materials and Design 30, 2009, p. 122–128
[6] G. Z. Wang, Y. N. Cheng, K. Becker, J. Wilde, Applying Anand Model to Represent the Viscoplastic Deformation Behavior of Solder Alloys, Journal of Electronic Packaging, Sep. 2001, Vol. 123, p. 247–253
[7] Darveaux R., Member, ZEEE and Kingshuk Banerji, Constitutive Relations for Tin-Based Solder Joints, IEEE transactions on components, hybrids and manufacturing technology, vol. 15, no 6, Dec. 1992
[8] Masazumi Amagai, Masako Watanabe, Masaki Omiya, Kikuo Kishimoto, Toshikazu Shibuya, Mechanical characterization of Sn–Ag-based lead-free solders, Microelectronics Reliability 42 (2002) 951–966
[9] Steffen Wiese, Ekkehard Meusel, Klaus-Juergen Wolter, TU Dresden, Microstructural Dependence of Constitutive Properties of Eutectic SnAg and SnAgCu Solders, 2003 Electronic Components and Technology Conference
[10] Viswanadham Colangelo, Preventing Passive Component Failures on PCBs, SMT magazine, February 1999, p. 64–68
[11] Josef Šandera, Design and Reliability of the Connection in 3D Electronic Systems, FEKT, VUT Brno, disertační práce, Brno 2004