Ať už si to přiznáme, či nikoli, z pozice člověka budeme závislí na mnoha věcech. Některé vazby přitom vnímáme pozitivně, další již v záporném slova smyslu, a ještě jiné třeba ani neřešíme. Se „závislostmi“ však nebojujeme sami, náš obor je jimi doslova protkán. Se spoustou z nich jsme se už stačili seznámit, a možná i smířit, jiné dokáží vývojáře překvapit i po letech. A proto je též řešíme, třeba jako změnu kapacity vícevrstvých keramických kondenzátorů MLCC (Multilayer Ceramic Capacitor) v závislosti na jejich předpětí (Bias Voltage).
Kapacita těchto prvků se s přivedeným stejnosměrným napětím prostě mění, a u některých typů dokonce i víme jak moc. Jedná se o důležitou informaci a činíme dobře, pokud ji nebereme na lehkou váhu. Pokud jsme se však rozhodli charakteristikám od výrobce z nějakého důvodu nevěřit, příp. se v našem konkrétním případě dokumentace „odmlčela“ nadobro, nezbývá než se poohlédnout po vlastním řešení. Není vůbec složité, a přesto s ním dosáhneme solidních výsledků. Pro pořádek jen dodejme, na čem budeme při měření takové závislosti sami závislí. Půjde o docela jednoduché zapojení s několika málo součástkami, které si vyrobíme třeba jako užitečný přípravek i do budoucna, a dále pak dva zdroje napájecího napětí spolu s voltmetrem.
Základní myšlenku popisuje Fons Janssen ze společnosti Maxim Integrated v nedávné aplikační poznámce s názvem How to Measure Capacity Versus Bias Voltage on MLCCs [1]. Smyslem našeho článku není její doslovný překlad, pouze zde ukážeme a okomentujeme to nejdůležitější.
Svůj měřicí přípravek zapojíme dle obr. 1. Někdo tomu říká „bastl“, my se ale za takový přístup určitě nestydíme – jedná se o běžnou praxi, kterou pozorujeme i ve firmách zvučných jmen.
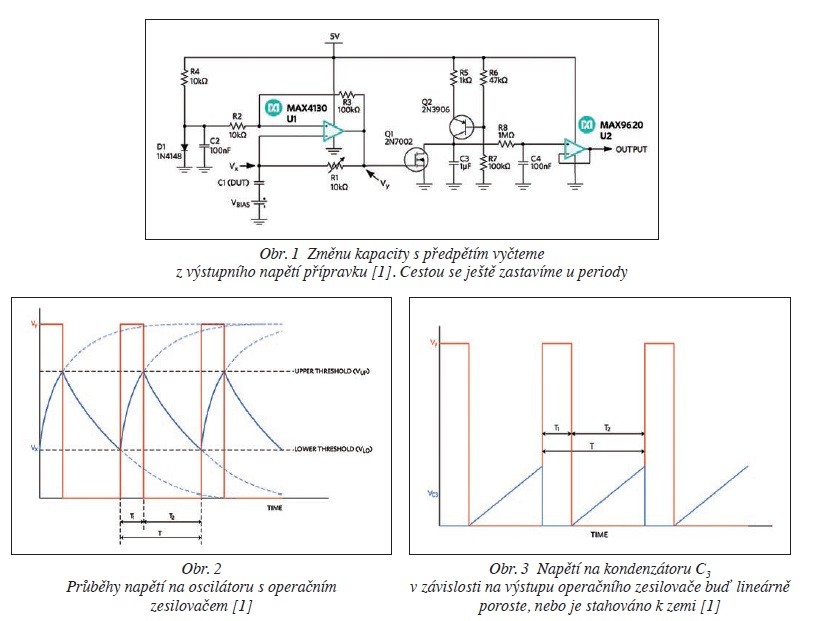
Zapojení staví na operačním zesilovači MAX4130 ve funkci komparátoru se zpětnovazebními rezistory R2 a R3 vnášejícími hysterezi. Díky definici úrovně nad zemí GND s diodou D1 se pak obejdeme ještě bez záporného napájení. Na invertující vstup dále zamíří zpětnovazební síť složená z prvků R1 a C1, a my tak dostáváme RC oscilátor. Jeho odpor bude stavitelný, kapacita pak naší měřenou součástkou DUT.
Pro vysvětlení funkce si nadefinujeme dva body – výstup operačního zesilovače jako Vy a spoj mezi členem RC coby Vx. Činnost obvodu pak sledujeme na obr. 2. Máme‑li výstup zesilovače na 5 V, dochází k nabíjení testované kapacity C1 přes potenciometr R1, dokud nedosáhneme horní meze, pak musí být výstup stažen k nule. Kondenzátor se nyní vybíjí, dokud opět nedosáhneme dolní meze, a zapojení si tak znovu na svém výstupu nevynutí 5 V. Děj se neustále opakuje, protože jsme právě vyrobili oscilátor.
Perioda kmitů bude záviset na velikosti odporu a kapacity spolu s prahovými úrovněmi VUP a VLO. Protože však uvažujeme konstantní napětí, mohou doby T1 spolu s T2 odpovídat přímo časové konstantě RC.
Abychom ale dokázali časový úsek popsat úměrným, a především pak snadno měřitelným napětím, přidáme ještě do našeho zapojení obvod s tranzistory Q1 a Q2. První MOSFET bude řízen přímo z výstupu operačního zesilovače, ve fázi T1 zůstane sepnutý a stahuje při tom napětí pomocného kondenzátoru C3 k zemi. V průběhu T2 je pak tranzistor Q1 vypnutý, a umožňuje tak zdroji konstantního proudu složenému z tranzistoru Q2 a jeho rezistorů R5, R6 a R7 nabíjet kapacitu C3. Lineárního průběhu zde dosáhneme vhodnou volbou kondenzátoru, přičemž s rostoucí dobou T2 napětí na C3 dále poroste – přesně tak, jak to vidíme na obr. 3.
A to je vše. S uvážením konstant proto prohlásíme napětí na kondenzátoru C3 úměrné době T2, a tudíž i na naší testované kapacitě C1. Zbývá už jen projít dolnopropustným filtrem složeným z R8 a C4, a vše ještě oddělit operačním zesilovačem U2 s nízkým offsetem. Nyní již můžeme připojit k výstupu voltmetr.
Abychom mohli na voltmetru odečítat pokles kapacity s rostoucím předpětím přímo v procentech, provádíme před započetím měření jednoduchou kalibraci popsanou v [1]. Také si ohlídáme případnou saturaci tranzistoru Q2. Aplikační poznámka zároveň ukazuje naměřené výsledky s náhodně vybraným kondenzátorem 10 μF, jehož pokles kapacity zkoumáme na základě měření výstupního napětí z našeho zapojení, a pro kontrolu ještě přesným čítačem prověříme periodu signálu. Ta se oproti výchozím 0 V po přivedení předpětí 5 V znatelně snížila, a odpovídá tak poklesu na 66,5 % výchozí kapacity. Na základě měření napětí jsme přitom stanovili stejný pokles na 0,671 V, tzn. 67,1 %. Zapojení pracuje a převádí správně.
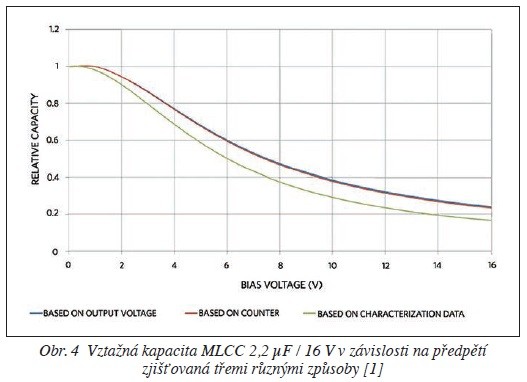
Ve druhém případě již do hry vstupuje známá kapacita Murata o velikosti 2,2 μF / 16 V a měření nyní probíhá v celém provozním rozsahu od 0 až do 16 V. Vztažnou kapacitu opět stanovujeme na základě výstupního napětí obvodu, dále pak jeho periody, a ke všemu ještě využijeme dat dostupných přímo od výrobce, přesně jak to autor vynáší na obr. 4. Naše dvojí měření bude prakticky totožné a pouze dokládá správnou činnost obvodu při převodu času na napětí, a to i v případě většího dynamického rozsahu. Oproti třetí charakteristice se sice mírně odlišujeme, nicméně trend zůstává zachován.
V článku jsme zdůraznili docela „zákeřnou“ vlastnost keramických kondenzátorů, které svou kapacitu mění s přiváděným napětím. Rozhodně se proto vyplatí prozkoumat, co nám o této skutečnosti prozradí sám výrobce, příp. si vše ověříme na vlastním voltmetru. Použijeme k tomu jednoduchý přípravek, dva zdroje a po základní kalibraci odečítáme pokles přímo v procentech [1]. Pak už nás nepřekvapí, když se z původního 4,7 μF, navzdory zaručované teplotní stabilitě keramické součástky, najednou stává 0,33 μF – přesně jak se nad tím podivoval další autor s mnohaletou praxí v [2].
[1] How to Measure Capacity Versus Bias Voltage on MLCCs, autor Fons Janssen, Maxim Integrated, https://www.maximintegrated.com/en/appnotes/index.mvp/id/6014
[2] Temperature and Voltage Variation of Ceramic Capacitors, or Why Your 4.7μF Capacitor Becomes a 0.33μF Capacitor, autor Mark Fortunato, Maxim Integrated, https://www.maximintegrated.com/en/app-notes/index.mvp/id/5527