Vést či nevést : otázka layoutu – část 1 – teorie
Otázka layoutu hraje v případě napájecích zdrojů a jejich vlastností významnou úlohu. Takový zdroj může být sice „papírově” navržen správně, samo o sobě to však ještě neznamená, že bude i v praxi pracovat tak, jak jsme původně zamýšleli. Vše se bude zkrátka odvíjet od náležitého provedení layoutu. V tomto článku se proto na důležité stránky návrhu plošného spoje pro napájecí zdroje podíváme podrobněji. Samotný výklad bude rovněž z velké části podepřen srovnávacím měřením, vycházejícím ze dvou identických napájecích zdrojů s odlišným motivem.
Základy – parazitní vlivy na desce plošného spoje
A) Stejnosměrný odpor
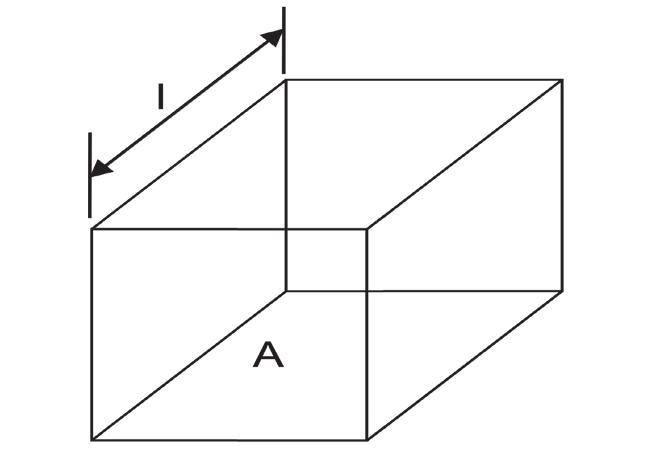
Obr. 1 Odpor trasy na desce plošného spoje
V případě napájecích zdrojů s vysokými výstupními proudy musíme uvažovat ztráty, způsobené odporovou povahou vodivé trasy, snižující dosahovanou účinnost, vnášející problémy, související s chlazením, a také ovlivňující regulaci výstupního napětí. Odpor dané trasy na desce plošného spoje lze stanovit následujícím způsobem:
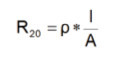
ρ: Měrný odpor materiálu, použitého
k výrobě trasy na desce plošného spoje
(1.7×10-8 Ωm pro měď při 20 °C)
l: Délka trasy na desce plošného spoje
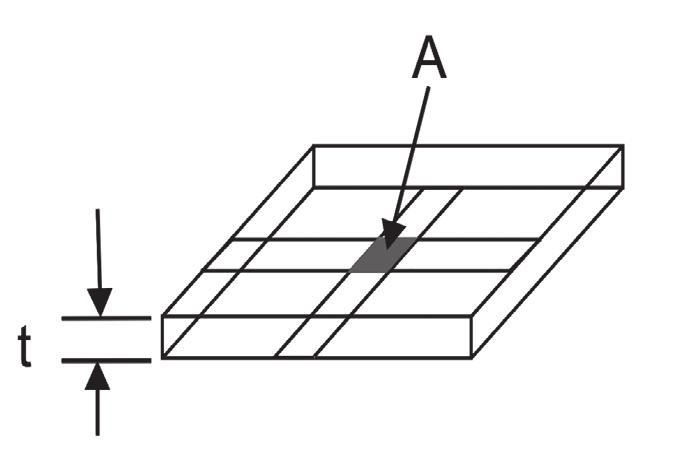
A: Plocha průřezu trasy na desce plošného spoje
Teplotní závislost odporu můžeme vyjádřit jako
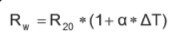
kde je
R20: Odpor trasy při 20 °C
α: Teplotní koeficient
ΔT: Nárůst teploty v Kelvinech
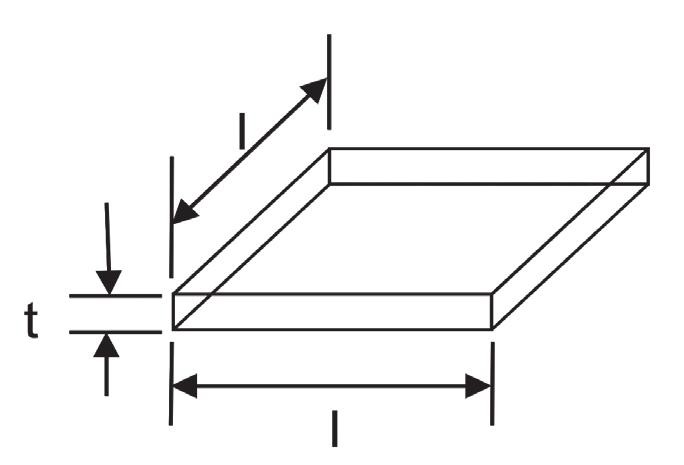
Obr. 2 Čtverec trasy
Výpočet odporu lze dále zjednodušit počítáním čtverců. Budeme přitom uvažovat, že délka i šířka jsou ve vzorci pro výpočet odporu totožné, tj. vzájemně se vyruší a odpor vodiče pak bude záviset pouze na tloušťce a měrném odporu materiálu (viz obr. 2). Místo toho, abychom měřili délku trasy, pak jenom spočítáme počet čtverců, které se do zkoumané trasy vejdou, přičemž výsledek ještě vynásobíme hodnotou z tab. 1.
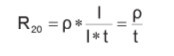
R20: Odpor trasy při 20 °C
ρ: Měrný odpor materiálu použitého
k výrobě trasy
t: Tloušťka trasy
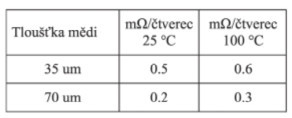
Tab. 1 Odpor/čtverec trasy
B) Impedance
Vedle DC odporu musíme v případě trasy na plošném spoji rovněž uvažovat induktivní AC složku, kterou lze stanovit hrubým odhadem (přibližně 6 nH/cm). Pokud navíc dochází ke křížení trasy se zemní plochou (GND), snižujeme induktivní reaktanci na 1/5, takže dostáváme něco okolo 1.2 nH/cm.
Obr. 3 Kapacita mezi vodiči
Budou-li dvě trasy procházet vzájemně nad sebou, vznikne mezi nimi parazitní kapacita. Na jedné straně to může vést k nežádoucím interferencím, na straně druhé však tímto způsobem výhodně potlačíme vysokofrekvenční rušení. Jako dielektrikum pro navrstvené vodiče přitom slouží materiál plošného spoje. Relativní permitivita materiálu plošného spoje je přibližně 4,8. Kapacitu dvou vrstvených vodičů pak můžeme určit následujícím způsobem:
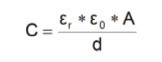
C: Kapacita mezi vodiči
εr: Relativní permitivita materiálu desky plošného spoje
ε0: Permitivita vakua
A: Plocha, kterou se trasy překrývají
d: Vzdálenost mezi dvěma trasami
Získané kapacity v řádech fF se mohou zdát malé. Nicméně, v případě synchronních snižujících měničů a jejich spínaných uzlů hovoříme o velmi vysokých rychlostech přeběhu v řádech až do 1 V na ns, takže s parazitní kapacitou o velikosti pouhého 1 pF můžeme vytvářet proud 1 mA. [1]
C) Prokovy
I v případě prokovů se setkáváme s parazitními odpory a indukčnostmi, podobnými těm, o kterých jsme již hovořili v souvislosti s deskami plošných spojů a jejich trasami. Odpor prokovu pak určíme následujícím způsobem:
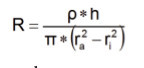
R: Odpor prokovu
ρ: Měrný odpor materiálu pro výrobu prokovu
h: Výška prokovu
ri: Vnitřní průměr
ra: Vnější průměr
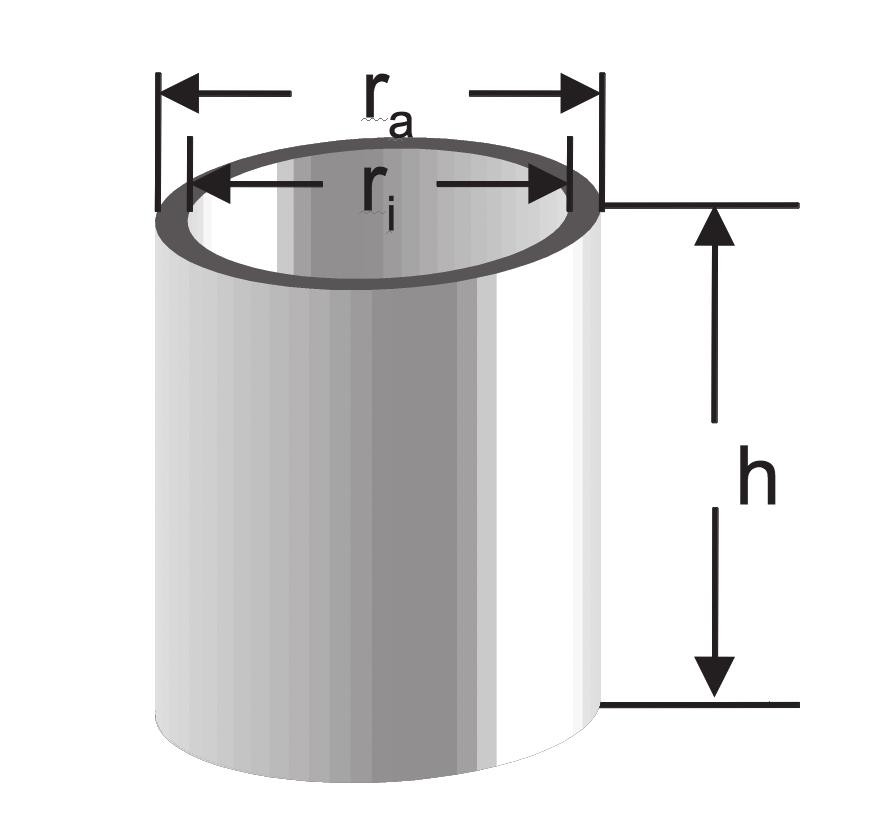
Obr. 4 Prokov, jeho geometrie a související výpočet odporu
Proudy tekoucí přes prokovy bývají zpravidla omezeny velikostí 1 až 3 A. Vedle vlastního ohmického odporu však musíme také zapracovat parazitní indukčnost prokovu, kterou lze zhruba vypočítat pomocí následujícího vzorce [3]:
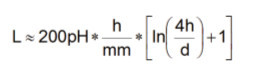
L: Indukčnost prokovu
h: Výška prokovu
d: Průměr prokovu
D) Proudové smyčky a indukčnost
Proudy se vždy uzavírají ve smyčce, takže může vznikat magnetické pole. Bude-li docházet ke změně proudu, rovněž tím ovlivníme intenzitu magnetického pole a generujeme napětí.
Velikost indukovaného napětí definuje Faradayův zákon takto:
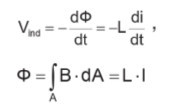
Indukčnost je rovněž ovlivňována geometrií použitého vodiče. Větší plocha přitom znamená větší indukčnost. Z Faradayova zákona dále vyplývá, že větší indukčnosti bude také odpovídat vyšší samoindukční napětí (uvažujeme přitom proudy se stejnou rychlostí přeběhu). Trasy a jejich smyčky, u kterých předpokládáme vysoké di/dt by z tohoto důvodu měly být dimenzovány tak, aby jimi uzavíraná plocha byla pokud možno co nejmenší. Napěťové překmity tak udržíme na nízké úrovni.
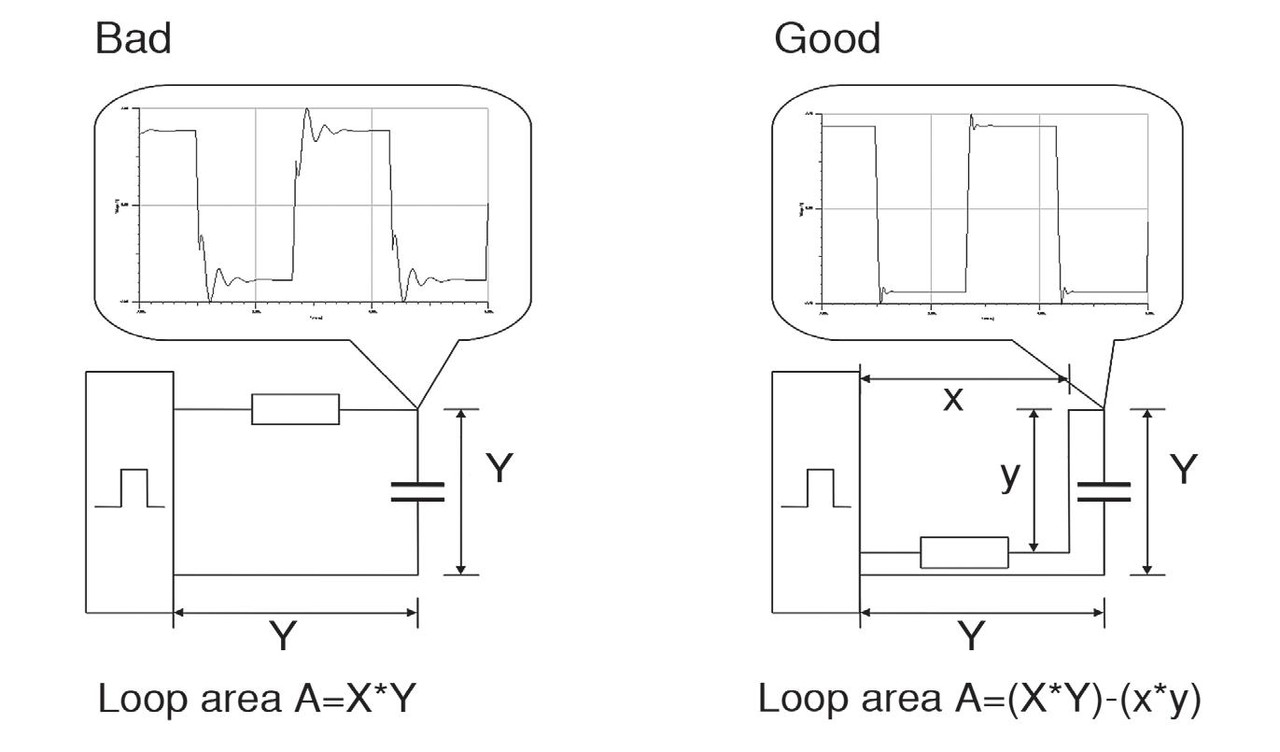
Obr. 5 Smyčka, její indukčnost a vliv na velikost překmitů
V příštím čísle časopisu: Pokyny pro správný návrh layoutu.
Literatura
[1] Robert Kollman, “Constructing Your Power Supply – Layout Considerations”, Texas Instruments Power Supply Design Seminar SEM1600, Topic 4, TI Literature number SLUP224 http://www-s.ti.com/sc/techlit/slup230.pdf
[2] Bill Andreycak, Bob Mammano,“Practical Considerations in Troubleshooting and Optimizing Power Supply Control Circuits and PCB”, Texas Instruments Online Seminar http://training.ti.com/courses/coursedescription.asp?iCSID=1150
[3] Prof. Dr. T. Wolf, „Schaltungstechnik“ Vorlesungsskript der Fachhochschule Landshut, http://www.fh-landshut.de/~wlf/schT/Vorlesung/ST_1.pdf
[4] Phil Rogers, “Board layout boosts power-supply performance”, Seite 175…178, EDN Magazine November 5, 1998, http://www.edn.com/archives/1998/110598/pdfs/23ms435.pdf




