Diferenční impedance aneb v čem je diference

Pokud si umíte spočítat Zo – charakteristickou impedanci plošných spojů na DPS, neměl by pro vás být problém ani návrh diferenciálního vedení plošných spojů s dodržením požadované hodnoty impedance. Co ale když řeknu, že „…společným vedením dvou signálových spojů můžeme upravit použitím obecných návrhových pravidel impedanci v hodnotě například 50 Ω na diferenciální impedanci cca 80 Ω“. Stále víte o čem je řeč?

Tento článek má za úkol přiblížit základní výpočty týkající se diferenční (rozdílové) impedance. Jeho cílem není nahrazení rozsáhlých teoretických rozborů, nýbrž jasná definice a použití v praxi.

Samostatný plošný spoj

Obr. 1 (a) ukazuje typické vedení s jedním plošným spojem. Takový spoj má na DPS charakteristickou impedanci Zo a protéká jím proud i. Napětí mezi spojem a libovolným bodem na desce je (podle Ohmova zákona) V=Zo·i.

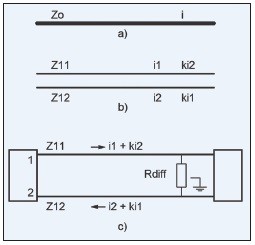
Obr. 1 Různé konfigurace plošných spojů

Obecný případ, dvojice plošných spojů

Na obr. 1 (b) je ukázka dvojice plošných spojů. Spoj Trace1 má charakteristickou impedanci Z11, což odpovídá hodnotě Zo z předchozího příkladu a protéká jím proud i1. Podobně je definován i druhý spoj Trace2. Jakmile dojde k přiblížení spoje Trace2 k Trace1, začne například z Trace2 téct proud do Trace1 a to s úměrnou konstantou k. Naprosto stejně se však chová i proud i1 z Trace1, který se stejnou konstantou začne ovlivňovat i proud v Trace2. Napětí na jednotlivých spojích je možné určit opět podle Ohmova zákona:

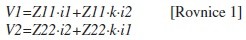
Nyní definujme Z12=k·Z11 a Z21=k·Z22. Podle rovnice 1 pak můžeme psát:

Toto je poměrně známá dvojice rovnic, která se často objevuje v odborné literatuře. Uvedené rovnice není problém dále upravit na libovolný počet spojů na desce a celek je možné vyjádřit ve formě matice, kterou jistě většina z vás zná.

Speciální případ, diferenciální vedení

Na obr. 1 (c) je uveden příklad diferenciálního páru plošných spojů. Stejně jako v případě rovnice 1 můžeme psát:

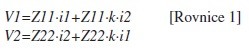
Nyní předpokládejme, že spoje jsou navržené kvalitně a že se jedná o vyvážený stav, tedy:

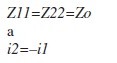
Z toho (s trochou matematiky) můžeme získat:

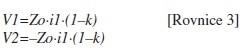
Všimněte si, že V1=–V2, což je přesně situace, která platí v případě diferenciálního vedení.

Reálná (odd mode) impedance

Napětí V1 je míněno vůči společné zemi. Reálná (nebo také efektivní) impedance pro plošný spoj Trace1 (pokud pracujeme buď v „odd mode“ v případě diferenciálních párů, nebo obecně, v případě samostatného spoje) má hodnotu rovnající se napětí děleného proudem, tedy:

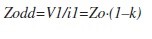
Jelikož Zo=Z11 a k=Z12/Z11, můžeme psát, že:

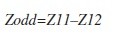
což je také poměrně známá rovnice, dostupná ve většině odborné literatury.

Vhodným zakončením diferenciálního vedení, které brání vzniku odrazů a stojatého vlnění, je rezistor s hodnotou Zodd. Podobný výpočet platí v tomto případě i pro spoj Trace2, který se chová podobně (v tomto speciálním případě vyváženého diferenciálního páru).

Diferenční (rozdílová) impedance

Předpokládejme, že jsme oba spoje diferenciálního páru zakončili pomocí rezistorů do společné země. Vzhledem k tomu, že i1=i2, neprotéká společnou zemí žádný proud. To je důvod, proč spojení diferenciálních vodičů pomocí odporů do země nemá žádný reálný důvod. Někteří lidé tvrdí, že propojení vodičů se zemí je důležité z důvodu izolace diferenciálního signálu od společného rušení. Typická konfigurace zakončovacího členu má však podobu podle obr. 1 (c). Pouze jediný rezistor mezi plošným spojem Trace1 a Trace2, jehož hodnota vychází ze součtu impedancí z předchozího odstavce, tedy:

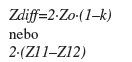
To je také důvod toho, proč se často v případě diferenciálního signálového páru uvádí hodnota impedance kolem 80 Ω, přičemž impedance jednotlivých plošných spojů je 50 Ω.

Výpočet

Myslíte si, že definice Zdiff jako 2·(Z11– Z12) není v našem případě praktická, protože neznáme hodnotu Z12? Ale pokud si vzpomínáte, tak hodnota Z12 je závislá na vzájemném koeficientu k. Více informací o jeho hodnotě je dostupných například v [1], kde se popisuje z pohledu přeslechu mezi signály. Podobně i společnost National Semiconductor zveřejnila základní vzorce pro výpočet hodnoty Zdiff, které postupem času zobecněly:

Zdiff=2·Zo[1–0.48·exp(–0.96·S/H)] (mikropáskového)

Zdiff=2·Zo[1–0.347·exp(–2.9·S/H)] (páskové vedení)

Kde všechny hodnoty vycházejí z obr. 2 a „exp()“ představuje základ přirozeného logaritmu, rozšířeného o hodnoty v závorkách. Zo vychází ze standardní definice.

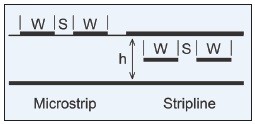
Obr. 2 Základní hodnoty pro výpočet diferenční impedance

Impedance ke společnému potenciálu

Jen jako příklad si uveďme i situaci, kdy impedanci vztahujeme ke společnému potenciálu (obvykle zemi). Zde je hlavní rozdíl v tom, že i1=i2 (tedy bez znaménka mínus), takže rovnice 3 má podobu:

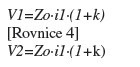
Ovšem opět V1=V2, jak by se dalo očekávat, stejně jako impedance jednotlivých spojů se rovná hodnotě Zo·(1+k). V tomto případě jsou však oba spoje zakončeny rezistorem do společné země, takže proud, který jí protéká je roven součtu i1+i2. Jelikož impedance spojů je shodná, chová se obvod jako v případě paralelního řazení obou rezistorů. Proto má také impedance společného bodu hodnotu pouze poloviční, tedy:

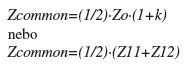
Všimněte si, že impedance je v tomto případě pouze ¼ hodnoty diferenční impedance u symetrického páru.