V rámci spolupráce s redakcí časopisu jsem byl požádán o několik článků o práci autorouteru. Vznikne tak seriál o propojovacích technikách a tricích, které jsou používány v algoritmech realizujících spojové obrazce. Dnešním dílem tedy začínáme. Nejprve formulace problému a několik pojmů používaných v dalším textu.
Je dán propojovací prostor definovaný rozměry, počtem vrstev, rozložením součástek nebo komponent na desce nebo čipu, trasami spojů již dříve navržených uživatelem, zónami pro zákaz průchodů nebo tras spojů. Známe tedy polohu všech vývodů komponent, které mohou mít nejrůznější tvar plošek a mohou být umístěny na libovolných vrstvách. Důležitým prvkem jsou návrhová pravidla – tedy požadavek uživatele na tloušťky vodičů a izolačních vzdáleností mezi nejrůznějšími páry elementů (pin–pin, pin–smd pin, pin–průchod (dále via)…). Všechna tato omezení, tvary a definice musí autorouter respektovat. Jeho úlohou je najít v takto definovaném prostoru propojení vývodů komponent dané seznamem spojů vygenerovaným ze schématu obvodu.
Obecně je tedy dána v prostoru množina spojů sestávající z vývodů komponent, které je potřeba propojit bez kolizí a křížení v maximální míře – nejlépe 100 %. S touto velmi složitou úlohou je spojeno hned několik problémů:
S přibývající složitostí obvodů a rozmanitostí součástek, jejich různých roztečí vývodů a velikostí plošek, tzn., že na propojovací ploše může být opravdu cokoliv, roste i požadavek na důmyslnost a komplexnost algoritmů, které popisovaný problém musí řešit. V poslední době se touto problematikou zabývá řada renomovaných universit a vzniká škála tzv. akademických autorouterů. Je to dáno potřebou a trendem, neboť složitost obvodů již začíná překračovat možnosti „lidského“ návrhu a také časové nároky, které by vyžadoval „ruční“ návrh, by byly neúměrně vysoké vzhledem k požadavkům na rychlost realizace. Je prostě doba elektroniky. K řešení jmenovaných úloh se používá teorie grafů, (zkoumá se planarita grafů, tedy možnosti navrhnout desku s co nejmenším počtem vrstev, počítají se tzv. minimální kostry spojů, což je spojnice všech vývodů spoje s minimální možnou délkou a další problémy).
Tolik na úvod. Dnes se podíváme na základní a nejpoužívanější vyhledávácí algoritmus – Lee – nazvaný po jeho tvůrci, jinak také „maze“ autorouter. Spočívá v rozdělení prostoru do mřížky (gridu) – viz obr. 1a, umístění překážek a vývodu do této mřížky a použitím prohledávací vlny, která, pokud cesta mezi startem (S) a cílem (T) existuje, tuto cestu najde a to dokonce nejkratší možnou. Algoritmus sestává ze 3 kroků:
 autorouter1a.jpg.jpeg) |  autorouter1b.jpg) |
| Obr. 1a Mřížka s umístěním překážek, startu S a cíle T | Obr. 1b Expanze vlny a dosažení cíle |
 autorouter1c.jpg.jpeg) |  autorouter1d.jpg.jpeg) |
| Obr. 1c Nalezení zpětné cesty | Obr. 1d Vyčištění vlny a doplnění překážek |
Pro ilustraci je popisovaná pouze 1 vrstva – plocha, mřížka však může být trojrozměrná a pro hledání cesty mezi objekty ležícími v různých vrstvách jsou používány průchody. Vzhledem k propojitelnosti mají jednotlivé vrstvy přiřazen preferovaný směr (vertikální nebo horizontální) a změny směrů jsou realizovány průchody – viz obr. 2.
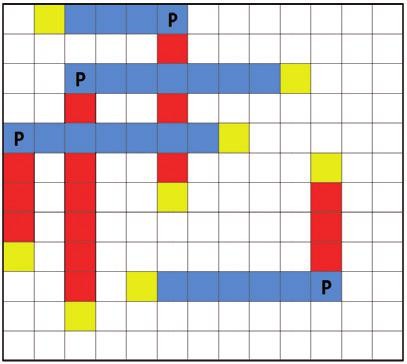 autorouter2.jpg.jpeg)
Obr. 2 Vícevrstvý model s uplatněním směrů. P – průchod mezi vrstvami
Vlna se šíří ze startu obsazením sousedních buněk vlevo, vpravo, nahoře a dole, pokud je buňka volná a přiřadí se jí číslo odpovídající počtu kroků expanze – viz obr. 1b a to tak dlouho, dokud není dosažen cíl (T) nebo vlna nezanikne tím, že již není kam expandovat, v tom případě úloha nemá řešení. V našem případě byl cíl nalezen v počtu kroků 19. Buňky určené k expanzi se uchovávají v zásobníku čelních buněk. Konstrukce zpětné cesty je jednoduchá, prostě se couvá z cíle po buňkách s klesajícím číslem vlny až do dosažení startu (obr. 1c, cesta označena tučnou konturou). Zbývá „uklidit“ mřížku pro další návrh a označit nalezenou cestu jako překážku pro další, ještě nenavržené cesty, což je naznačeno na obr. 1d.
Uvedený model hledání cesty má samozřejmě mnoho variant, které vedou k úspoře paměti, ke zrychlení práce algoritmu, třeba tím, že se vlny šíří ze startu a cíle proti sobě, tím se ušetří zhruba polovina času na prohledávání.
Tento algoritmus je geniální svou jednoduchostí, protože pokud existuje řešení, algoritmus ho nalezne a to dokonce to nejlepší a nejkratší. Nicméně to platí pouze v jednoduchém, právě popsaném případě. Jinak je algoritmus neefektivní, protože prohledává všechny možnosti, což vede k velkým časovým nárokům na výpočet. Toto omezení trochu smazávají svou výkonností dnešní počítače z hlediska rychlosti i paměti. Při řešení a návrhu čipu, kde jsou biliony komponent, se ale čas výpočtu a nároky na paměť stávají při použití Leeova algoritmu kritickými faktory.
V příštím díle seriálu přiblížíme další propojovací techniku – kanálové a paprskové algoritmy.